
题目列表(包括答案和解析)
设椭圆  :
: (
( )的一个顶点为
)的一个顶点为 ,
, ,
, 分别是椭圆的左、右焦点,离心率
分别是椭圆的左、右焦点,离心率
 ,过椭圆右焦点
,过椭圆右焦点
 的直线
的直线  与椭圆
与椭圆  交于
交于 ,
, 两点.
两点.
(1)求椭圆 的方程;
的方程;
(2)是否存在直线  ,使得
,使得
 ,若存在,求出直线
,若存在,求出直线
 的方程;若不存在,说明理由;
的方程;若不存在,说明理由;
【解析】本试题主要考查了椭圆的方程的求解,以及直线与椭圆的位置关系的运用。(1)中椭圆的顶点为 ,即
,即 又因为
又因为 ,得到
,得到 ,然后求解得到椭圆方程(2)中,对直线分为两种情况讨论,当直线斜率存在时,当直线斜率不存在时,联立方程组,结合
,然后求解得到椭圆方程(2)中,对直线分为两种情况讨论,当直线斜率存在时,当直线斜率不存在时,联立方程组,结合 得到结论。
得到结论。
解:(1)椭圆的顶点为 ,即
,即
 ,解得
,解得 ,
,
 椭圆的标准方程为
椭圆的标准方程为 --------4分
--------4分
(2)由题可知,直线 与椭圆必相交.
与椭圆必相交.
①当直线斜率不存在时,经检验不合题意. --------5分
②当直线斜率存在时,设存在直线 为
为 ,且
,且 ,
, .
.
由 得
得 , ----------7分
, ----------7分
 ,
, ,
,

=
所以 ,
----------10分
,
----------10分
故直线 的方程为
的方程为 或
或
即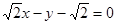 或
或
| 3 |
| 3 |
| ||||
| 2 |
| ||||
| 2 |
某医疗研究所为了检验某种血清预防感冒的作用,把![]() 名使用血清的人与另外
名使用血清的人与另外![]() 名未用血清的人一年中的感冒记录作比较,提出假设
名未用血清的人一年中的感冒记录作比较,提出假设![]() :“这种血清不能起到预防感冒的作用”,利用
:“这种血清不能起到预防感冒的作用”,利用![]() 列联表计算得
列联表计算得![]() ,经查对临界值表知
,经查对临界值表知![]() .
.
对此,四名同学做出了以下的判断:
p:有![]() 的把握认为“这种血清能起到预防感冒的作用”
的把握认为“这种血清能起到预防感冒的作用”
q:若某人未使用该血清,那么他在一年中有![]() 的可能性得感冒
的可能性得感冒
r:这种血清预防感冒的有效率为![]()
s:这种血清预防感冒的有效率为![]()
则下列结论中,正确结论的序号是 .(把你认为正确的命题序号都填上)
(1) p∧﹁q ; (2)﹁p∧q ;
(3)(﹁p∧﹁q)∧(r∨s); (4)(p∨﹁r)∧(﹁q∨s)
有一道解三角形的题,因为纸张破损,在划横线地方有一个已知条件看不清.具体如下:在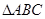 中角
中角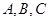 所对的边长分别为
所对的边长分别为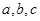 ,已知角
,已知角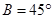 ,
,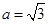 , ▲ ,求角
, ▲ ,求角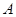 .若已知正确答案为
.若已知正确答案为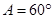 ,且必须使用所有已知条件才能解得,请你写出一个符合要求的已知条件.
,且必须使用所有已知条件才能解得,请你写出一个符合要求的已知条件.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com