
题目列表(包括答案和解析)
| OA |
| OC |
| AB |
| OM |
| AM |
| CM |
| BM |
| 1 |
| 2 |
| OM |
| AM |
| OA |
| OC |
| AB |
| OM |
| AM |
| CM |
| BM |
| 1 |
| 2 |
| OM |
| AM |
已知平面上的动点P(x,y)及两定点A(-2,0),B(2,0),直线PA,PB的斜率分别是k1,k2,且k1·k2=- .
.
(1)求动点P的轨迹C的方程;
(2)已知直线l:y=kx+m与曲线C交于M,N两点,且直线BM、BN的斜率都存在,并满足kBM·kBN=- ,求证:直线l过原点.
,求证:直线l过原点.
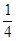 .
.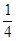 ,求证:直线l过原点.
,求证:直线l过原点.若数列{an}为等差数列,且am=x,an=y(m≠n,m,n∈N+),则am+n=![]() .现已知数列{bn}(bn>0,n∈N+)为等比数列,且bm=x,bn=y(m≠n,m,n∈N+),类比以上结论,可得到什么结论?你能说明结论的正确性吗?
.现已知数列{bn}(bn>0,n∈N+)为等比数列,且bm=x,bn=y(m≠n,m,n∈N+),类比以上结论,可得到什么结论?你能说明结论的正确性吗?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com