
题目列表(包括答案和解析)
(本小题12分)已知函数![]() 在定义域
在定义域![]() 上是奇函数,又是减函数。
上是奇函数,又是减函数。
(1)证明:对任意的![]() ,有
,有![]()
(2)解不等式![]() 。
。
(本小题12分)已知函数 是定义在
是定义在 上的偶函数,已知
上的偶函数,已知 时,
时, .
.

(1)画出偶函数 的图象;
的图象;
(2)根据图象,写出 的单调区间;同时写出函数的值域.
的单调区间;同时写出函数的值域.
(本小题12分)
已知函数 是定义在
是定义在 上的偶函数,当
上的偶函数,当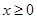 时,
时,
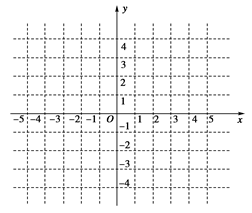
(1)求函数 的解析式,并画出函数
的解析式,并画出函数 的图像。
的图像。
(2)根据图像写出的单调区间和值域。
 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时,

 的解析式,并画出函数
的解析式,并画出函数 的图像。
的图像。(本小题12分)已知函数
 。
。
(1)当 时,判断
时,判断 的单调性;
的单调性;
(2)若 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数 的取值范围;
的取值范围;
一、选择题:本大题共12小题,每小题5分,共60分,将每小题给出的四个选项中的唯一正确的选项填在答题卡相应的题号中。
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
B
D
A
C
D
A
D
D
A
D
B
|