题目列表(包括答案和解析)
（本小题满分12分）将一枚质地均匀的骰子（形状为正四面体，四个面上分别标有数字
1，2，3，4的玩具）先后抛掷两次，观察抛掷后不能看到的数字的点数依次为
．
（1）求
的概率；（2）试将右侧求（1）中概率P的基本语句补充完整；（3）将a,b,3的值分别作为三条线段的长，求这三条线段能围成等腰三角形的概率．
（本题满分12分） 将一枚质地均匀且四个面上分别标有1，2，3，4的正四面体先
后抛掷两次，其底面落于桌面上，记第一次朝下面的数字为
，第二次朝下面的数
字为
。用
表示一个基本事件。
请写出所有的基本事件；
求满足条件“
为整数”的事件的概率；
求满足条件“
”的事件的概率。
（本小题满分12分）
将边长为2的正方形ABCD沿对角线BD折叠，使得平面ABD⊥平面CBD，AE⊥平面ABD，且AE＝
．
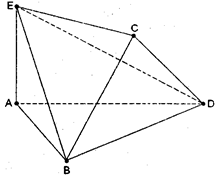
（Ⅰ）求证：DE⊥AC；
（Ⅱ）求DE与平面BEC所成角的正弦值；
（Ⅲ）直线BE上是否存在一点M，使得CM∥平面ADE，若存在，求点M的位置，不存在请说明理由．
|
（1）写出y关于x的函数关系式；
（2）如何设计x的大小，使得水箱的容积最大？
（本题12分）
有一种舞台灯，外形是正六棱柱，在其每一个侧面 (编号为①②③④⑤⑥)上安装5只颜色各异的灯，假若每只灯正常发光的概率为0.5，若一个侧面上至少有3只灯发光，则不需要更换这个面，否则需要更换这个面，假定更换一个面需要100元，用
表示更换的面数，用
表示更换费用。
（1）求①号面需要更换的概率；
（2）求6个面中恰好有2个面需要更换的概率；
（3）写出的分布列，求的数学期望。
2008．9
一、（每题5分，共60分）
1.B 2.B 3.B 4.C 5.C 6.A 7.D 8.B 9.A 10.C 11.D 12.B
二、（每题5分，共20分）
13.若
则
14.
15.15人 16.20
三、17.（10分）
④当
时，有
综上所述，m 的取值范围为
……………………………………………………………（10分）
18.（12分）
解：求导得：
，由于
的图象与直线
相切于点（1，-11）所以有
即：
……………………………………………………………………………（8分）
解得
………………………………………………………（10分）
所以
………………………………………………（12分）
19.（12分）
解：（1）当
时，不等式化为：
即
…………………（2分）（2）当
时，原不等式可化为：
当
时，有
∵
∴
…………（4分）
当
时，原不等式可化为：
①当
即
时有
②当
即
时
③当
即
时
………………………………………（10分）
20.（12分）
解：设剪去的小正方形边长为x┩，则铁盒的底面边长分别为：
┩，
┩，所以有 
得
…………（2分）
设容积为U，则
…………（4分）
则
令
得
或
（舍去）………（8分）当
时，
当
时，
∴当时，
取得极大值，即的最大值为18………………（11分）
所以剪去的小正方形边长为1┩时，容积最大，最大容积为18
……………………………………………………………………（12分）
21.（12分）
解：函数的导数
令
得或
………………………………………………………………（2分）
当
时，即
时,函数在
上为增函数,不合题意。
……………………………………………………………（4分）
当
时，即
时，函数在
上为增函数，在
内为减函数，在
上为增函数……………………………………（8分）
依题应有当
时
；当
时
所以：
，解得
，因此所求
范围为
………………（12分）
22.（12分）
（Ⅰ）设
，则
对于
都有
等价于
对于恒成立。………………（2分）
∴只需
在上的最小值
即可
∴
与
的关系如下表：
-3
（-3，-1）
-1
（-1，2）
2
（2，3）
3
+
0
-
0
+
-45+k
增
7+k
减
-20+k
增
-9+k
于是的最小值为
,所以
，即
为所求…………………………………………………………………………（6分）
（Ⅱ）对任意
都有“
”
等价于“
的最大值小于或等于
在
的最小值”……………………………………………………………………（8分）
下面求在上的最小值
列表
-3
（-3，-1）
-1
3
+
0
-
0
+
-21
增
-1
减
增
111
∴在上的最小值为－21，又
在内最大值为
于是
∴
为所求。
………………………………………………………………（12分）
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com