练习册

  • 练习册
  • 试题
    记该数组为:, 【查看更多】

     

    题目列表(包括答案和解析)

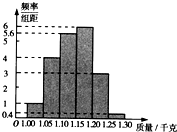    精英家教网为了了解一个小水库中养殖的鱼有关情况，从这个水库中多个不同位置捕捞出100条鱼，称得每条鱼的质量（单位：千克），并将所得数据分组，画出频率分布直方图（如图所示）
    （Ⅰ）在表格中填写相应的频率；
    分组 频率
    [1.00，1.05）
    [1.05，1.10）
    [1.10，1.15）
    [1.15，1.20）
    [1.20，1.25）
    [1.25，1.30]
    （Ⅱ）估计数据落在（1.15，1.30）中的概率为多少；
    （Ⅲ）将上面捕捞的100条鱼分别作一记号后再放回水库，几天后再120条鱼，其中带有记号的鱼有6条，请根据这一情况来估计该水库中鱼的总条数．

    查看答案和解析>>

    为了了解《中华人民共和国道路交通安全法》在学生中的普及情况，调查部门组织了一次知识竞赛，现随机抽取了某校20名学生的测试成绩，得到如图所示茎叶图：
    （1）若测试成绩不低于90分，则称为“优秀成绩”，求从这20人中随机选取3人，至多有1人是“优秀成绩”的概率；
    （2）以这20人的样本数据来估计整个学校的总体数据，若从该校（人数很多）任选3人，记ξ表示抽到“优秀成绩”学生的人数，求ξ的分布列及数学期望．

    查看答案和解析>>

    为了解某市民众对政府出台楼市限购令的情况，在该市随机抽取了50名市民进行调查，他们月收入（单位：百元）的频数分布及对楼市限购令赞成的人数如下表：
    月收入 [15，25） [25，35） [35，45） [45，55） [55，65） [65，75]
    频数 5 10 15 10 5 5
    赞成人数 4 9 12 5 1 1
    将月收入不低于55的人群称为“高收入族”，月收入低于55的人群称为“非高收入族”．
    （1）根据已知条件完成下面的2×2列联表，问是否有99.5%的把握认为收入与赞成楼市限购令有关？
    非高收入族 高收入族 总计
    赞成
    不赞成
    总计
    （2）现从月收入在[15，25）和[25，35）的两组人群中各随机抽取两人进行问卷调查，记参加问卷调查的4人中不赞成楼市限购令的人数为ξ，求随机变量ξ的分布列和数学期望．
    附：K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    ，n=a+b+c+d
    P（K2≥k0） 0.025 0.010 0.005
    k0 5.024 6.635 7.879

    查看答案和解析>>

    为了让人们感知丢弃塑料袋对环境造成的影响，某班环保小组的六名同学记录了自己家中一周内丢的塑料袋的数量，结果如下（单位：个）：
    33、25、28、26、25、31．如果该班有45名学生，那么根据提供的数据估计本周全班同学各家共丢弃塑料袋（　　）

    查看答案和解析>>

    为了让人们感受到丢弃塑料袋对环境造成的影响，某班环保小组的六名同学记录了自己家中一周内丢弃的塑料袋的数量，结果如下(单位：个)：33、25、28、26、25、31，如果该班有45名同学，那么根据提供的数据估计这周全班同学各家总共丢弃塑料袋的数量约为

    Ａ．900     Ｂ．1080        Ｃ．1260        Ｄ．1800

     

    查看答案和解析>>

     

    一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．

    １．Ａ　　　２．B　　 　３．Ｃ　　　４．A　　　５．B

    ６．Ｄ　　　７．Ａ　　　８．Ｃ　　　９．D　　　10．C

     

    二、填空题：本大题共4小题，每小题4分，共16分．

    11.    12.    13.或    14.

    15.       16.(也可表示成)    17.①②③

     

    三、解答题：本大题共6小题，共74分．

    18.解：(Ⅰ)由

                                             ---------4分

    由，得

    即

    则，即为钝角，故为锐角，且

    则

    故．                                     ---------8分

    (Ⅱ)设，

    由余弦定理得

    解得

    故．                        ---------14分

     

    19.解：(Ⅰ)由，得面

    则平面平面，

    由平面平面,

    则在平面上的射影在直线上,

    又在平面上的射影在直线上,

    则在平面上的射影即为点,

    故平面．                                 --------6分

    (Ⅱ)连接,由平面，得即为直线与平面所成角。

    在原图中，由已知，可得

    折后，由平面，知

    则，即

    则在中，有，，则，

    故

    即折后直线与平面所成角的余弦值为．       --------14分

     

    20.解：(Ⅰ)由，

    得

    又，故

    故数列为等比数列；                       --------6分

     

     

     

    (Ⅱ)由(Ⅰ)可知，

    则

    则对任意的恒成立

    由不等式对恒成立，得

    ．           --------14分

     

    21.解：

    (Ⅰ)由已知可得

    此时，                                 --------4分

    由得的单调递减区间为；----7分

    (Ⅱ)由已知可得在上存在零点且在零点两侧值异号

    ⑴时，，不满足条件；

    ⑵时，可得在上有解且

    设

    ①当时，满足在上有解

    或此时满足

    ②当时，即在上有两个不同的实根

    则无解

    综上可得实数的取值范围为.           --------15分

     

    22.解：(Ⅰ)(?)由已知可得，

    则所求椭圆方程.　　　　　　　　　　--------3分

    (?)由已知可得动圆圆心轨迹为抛物线，且抛物线的焦点为，准线方程为，则动圆圆心轨迹方程为.     --------6分

    (Ⅱ)由题设知直线的斜率均存在且不为零

    设直线的斜率为，，则直线的方程为：

    联立

    消去可得                 --------8分

    由抛物线定义可知:

    -----10分

    同理可得                                --------11分

    又

    (当且仅当时取到等号)

    所以四边形面积的最小值为.                   --------15分

     

     


    同步练习册答案