
题目列表(包括答案和解析)
如图,已知四棱锥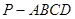 的底面为菱形,
的底面为菱形,
 面
面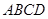 ,且
,且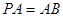 ,
,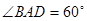 ,
,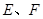 分别是
分别是 的中点.
的中点.
(1)求证: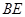 ∥平面
∥平面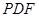 ;
;
(2)过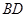 作一平面交棱
作一平面交棱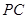 于点
于点 ,若二面角
,若二面角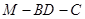 的大小为
的大小为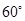 ,求
,求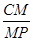 的值.
的值.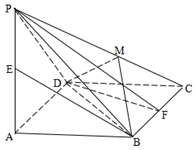
 的底面为菱形,
的底面为菱形,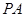
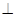 面
面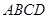 ,且
,且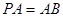 ,
,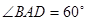 ,
,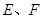 分别是
分别是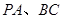 的中点.
的中点.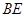 ∥平面
∥平面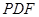 ;
;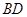 作一平面交棱
作一平面交棱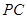 于点
于点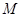 ,若二面角
,若二面角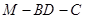 的大小为
的大小为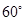 ,求
,求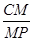 的值.
的值.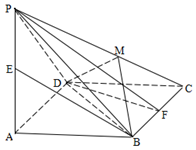
如图,已知四棱锥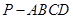 的底面的菱形,
的底面的菱形,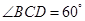 ,点
,点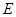 是
是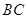 边的中点,
边的中点,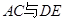 交于点
交于点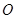 ,
,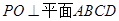
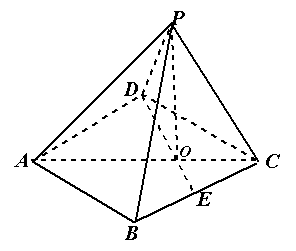
(1)求证: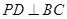 ;
;
(2)若 的大小;
的大小;
(3)在(2)的条件下,求异面直线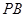 与
与 所成角的余弦值。
所成角的余弦值。
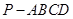 的底面的菱形,
的底面的菱形,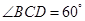 ,点
,点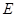 是
是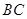 边的中点,
边的中点,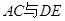 交于点
交于点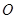 ,
,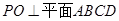
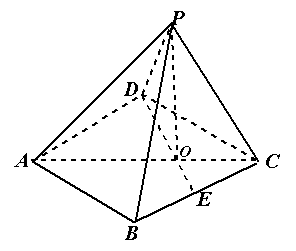
 ;
;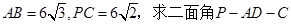 的大小;
的大小;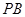 与
与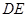 所成角的余弦值。
所成角的余弦值。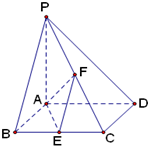 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E,F分别是BC,PC的中点.
| ||
| 2 |
一、选择题:
题号
答案
4、解析:与直线 垂直的切线
垂直的切线 的斜率必为4,而
的斜率必为4,而 ,所以,切点为
,所以,切点为 .切线为
.切线为 ,即
,即 ,答案:
,答案: .
.
5、解析:由一元二次方程有实根的条件 ,而
,而 ,由几何概率得有实根的概率为
,由几何概率得有实根的概率为 .答案:
.答案: .
.
6、解析:如果两条平行直线中的一条垂直于一个平面,那么另一条也垂直于这个平面,所以 正确;如果两个平面与同一条直线垂直,则这两个平面平行,所以
正确;如果两个平面与同一条直线垂直,则这两个平面平行,所以 正确;
正确;
如果一个平面经过了另一个平面的一条垂线,则这两个平面平行,所以 也正确;
也正确;
二、填空题:
题号
答案
 :
: 由点到直线的距离公式得圆心到直线的距离为
由点到直线的距离公式得圆心到直线的距离为 ,所以要求的最短距离为
,所以要求的最短距离为 .
.
三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.
解得 .………………………………………………………………… 6分
.………………………………………………………………… 6分
18、解:
(1)解法一:“有放回摸两次,颜色不同”指“先白再黑”或“先黑再白”,
记“有放回摸球两次,两球恰好颜色不同”为事件 ,………………………2分
,………………………2分
解法二:“有放回摸取”可看作独立重复实验, …………………………2分
… 10分
19、(1)证明: 连结 ,
, 与
与 交于点
交于点 ,连结
,连结 .………………………1分
.………………………1分
 (2)解法一:
(2)解法一:
解法二:如图,以点 为坐标原点,线段
为坐标原点,线段 的垂直平分线所在直线为
的垂直平分线所在直线为 轴,
轴, 所在直线为
所在直线为 轴,
轴, 所在直线为
所在直线为 轴,建立空间直角坐标系,令
轴,建立空间直角坐标系,令 ,……………2分
,……………2分
20、解:圆 的方程为
的方程为 ,则其直径长
,则其直径长 ,圆心为
,圆心为 ,设
,设 的方程为
的方程为 ,即
,即 ,代入抛物线方程得:
,代入抛物线方程得: ,设
,设 ,
,

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com