题目列表(包括答案和解析)
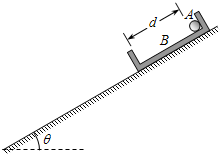（2010?汕头一模）如图所示，在倾角θ=30°的斜面上放置一段凹槽B，B与斜面间的动摩擦因数μ=
| ||
| 6 |
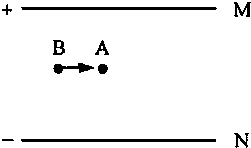（2003?徐州一模）如图所示，两块金属板M、N上下水平放置，两板间电压为U，有两个质量相等的小球A和B，带电A球静止在距下极板32cm处，B球不带电，以0.2m/s的水平速度与A球相碰，碰撞中无能量损失，在两球分离的瞬间把板间电压降为0.9U，碰后B球带电量可忽略不计．求：A、B在板上第一次撞击点间的距离．（ g取10m/s2）
如图所示，长为L的细绳上端系一质量不计的环，环套在光滑水平杆上，在细线的下端另一个质量为m的铁球（可视作质点），球离地的高度h=L，当绳受到大小为3mg的拉力时就会断裂．现让环与球一起以v=| 2gL |
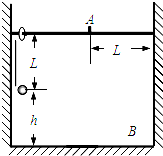
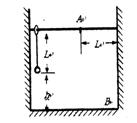
如图所示，长为L的细绳上端系一质量不计的环，环套在光滑水平杆上，在细线的下端另一个质量为m的铁球（可视作质点），球离地的高度h=L，当绳受到大小为3mg的拉力时就会断裂．现让环与球一起以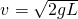
的速度向右运动，在A处环被挡住而立即停止，A离右墙的水平距离也为L．不计空气阻力，已知当地的重力加速度为g，试求：如图所示，长为L的细绳上端系一质量不计的环，环套在光滑水平杆上，在细线的下端另一个质量为m的铁球（可视作质点），球离地的高度h=L，当绳受到大小为3mg的拉力时就会断裂。现让环与球一起以
的速度向右运动，在A处环被挡住而立即停止，A离右墙的水平距离也为L.不计空气阻力，已知当地的重力加速度为g，试求：
（1）在环由运动到被挡住而立即停止瞬间绳对小球的拉力大小如何变化？变化了多少？
（1）在环停止以后的运动过程中，铁球的第一次碰撞点离墙角B点的距离是多少？
一．不定项选择题
1.BCD 2.B 3.AC 4.BC 5.B 6.A
二．实验题
1．
设A物块碰撞B物块前后的速度分别为v1和v2，碰撞过程中动量守恒，
代入数据得： 
（4分）
2.①14.45－14.50（4分）， ②C（4分），③1.01－1.02 。（4分）
三．计算题
1、
解：（1）设A球与B球碰撞前瞬间的速度为v0，
由动能定理得， 
①……………………（2分）
解得：
②
………………………（2分）
碰撞过程中动量守恒
③………………（2分）
机械能无损失，有 
④……………（2分）
解得
负号表示方向向左 ………………（1分）
方向向右 ……………………………（1分）
（2）要使m与M第二次迎面碰撞仍发生在原位置，则必有A球重新回到O处所用的时间t恰好等于B球的
………………………………（1分）
⑥ …………………………………………………………………（1分）
（n=0 、1 、2 、3 ……） ⑦ …………………………（2分）
由题意得： 
⑧ …………………………（1分）
解得： 
（n=0 、1 、2 、3 ……） ⑨ ……………（2分）
2．
解：子弹穿过A时，子弹与A动量守恒，
由动量守恒定律： ……………………… ① 3分
而由 得：v1=300m/s
得： ………………………②
子弹穿过B时， 子弹与B动量守恒，
由动量守恒定律： ………………………③ 3分
又由 …………………④ 2分
得：v2=100m/s
由③，④得： ………………………⑤
子弹穿过B以后，弹簧开始被压缩，A、B和弹簧所组成的系统动量守恒
由动量守恒定律： ………………………⑥ 3分
由能量关系： ……………………⑦ 3分
由② ⑤ ⑥ ⑦得： ………………………⑧ 2分
3.
解(1) 
与
第一次碰撞前，A、B之间的压力等于A的重力，即
…………1分
A对B的摩擦力
…………………………………………1分
而B与地面间的压力等于A、B重力之和，即
…………1分
地面对B的最大静摩擦力 
……………………………….1分
故与第一次碰撞前，B不运动………………………2分
（2）设A第一次碰前速度为v，碰后B的速度为v2
则由动能定理有………………………………………………………………..1分
……………………………………..2分
碰撞过程中动量守恒…………………………………………………………..1分
有 
………………………………………………..2分
解得
………………………………………………….2分
（3）当停止运动时， 继续向右滑行
（
）后停止，设B停止时，的速度为
，则由动能定理……………………………………………………………………1分
得
……………………………………………………..2分
解得
…………………………………………………………………..1分
4．
答案：（1）整个过程中系统克服摩擦力做的总功为
Wf＝µmgl（1＋2＋3＋…＋n）＝
…………………………..2分
整个过程中因碰撞而损失的总动能为
……………………………..1分
（2）设第i次（i≤n－1）碰撞前瞬间，前i个木块粘合在一起的速度为vi，
动能为 
与第i＋１个（i≤n－1）木块碰撞粘合在一起后瞬间的速度为vi＇，
由动量守恒定律 
………………………………………….2分
则
第i次（i≤n－1）碰撞中损失的动能为
…….2分
则第i次（i≤n－1）碰撞中损失的动能与碰撞前动能之比为
（i≤n－1）………………………………………………………1分
（3）n＝４时，共发生了i＝3次碰撞．
第1次碰前瞬间的速度为
，碰撞中动量守恒：
第1次碰后瞬间的速度为
……………………….3分
第2次碰前瞬间的速度为
碰撞中动量守恒：
第2次碰后瞬间的速度为
……………………….3分
第3次碰前瞬间的速度为
碰撞中动量守恒：
第3次碰后瞬间的速度为
………………………...3分
最后滑行到桌边，速度恰好为零，则
……………………….1分
即
整理后得
，代入数据解得
………………………….1分
5.
 |
6．
解：（1）在弹簧弹开的过程中系统动量守恒，假设A运动的方向为正方向，则
Mv1-mv2=0 2分
设从弹开到相遇所需时间为t，则有：
v1t+v2t=2πR 2分
联立以上两式得： 
2分
所以A球转过的角度为θ=120° 2分
（2）以A、B及弹簧组成的系统为研究对象，在弹簧张开的过程中，系统机械能守恒，则有
2分
Mv1-mv2=0 2分
解得： v1=2m/s，v2=4m/s 2分
所以，小球B在运动过程中受到光滑轨道的侧压力是其所需向心力，即：
2分
7．
解：（1）A与B第一次碰撞前，A对B的摩擦力为
2分
地面对B的最大静摩擦力为
2分
故A与B第一次碰撞前，B不运动
2分
（2）设A第一次碰前速度为v，碰后B的速度为v2，则由动能定理有
2分
碰撞过程中动量守恒有
2分
解得 2分
8．
(1)设A与B碰撞前A的速度为 V1 ，碰撞过程动量守恒，有：
mv1=(M+m)v (2分) 代入数据解得：v1=
（2）对A，从开始运动至碰撞B之前，根据动能定理，有：
（2分） 代入数据解得：
9．
（1）设物体从A滑落至B时速率为
(2分)
(1分)
物体与小球相互作用过程中，系统动量守恒，设共同速度为
(2分)
(1分 )
（2）设二者之间的摩擦力为
(2分)
(2分)
得
(1分)
（3）设物体从EF滑下后与车达到相对静止，共同速度为v2相对车滑性的距离为S1，
车停后物体做匀减速运动，相对车滑行距离为S1
(1分)
(1分)
(2分)
联立解得
(1分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com