
题目列表(包括答案和解析)
(本题满分18分,其中第1小题5分,第2小题5分,第3小题8分)
在平面直角坐标系中,已知![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,其中
,其中![]() 且
且![]() .设
.设![]() .
.
(1)若![]() ,
,![]() ,
,![]() ,求方程
,求方程![]() 在区间
在区间![]() 内的解集;
内的解集;
(2)若点![]() 是过点
是过点![]() 且法向量为
且法向量为![]() 的直线
的直线![]() 上的动点.当
上的动点.当![]() 时,设函数
时,设函数![]() 的值域为集合
的值域为集合![]() ,不等式
,不等式![]() 的解集为集合
的解集为集合![]() . 若
. 若![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(3)根据本题条件我们可以知道,函数![]() 的性质取决于变量
的性质取决于变量![]() 、
、![]() 和
和![]() 的值. 当
的值. 当![]() 时,试写出一个条件,使得函数
时,试写出一个条件,使得函数![]() 满足“图像关于点
满足“图像关于点![]() 对称,且在
对称,且在![]() 处
处![]() 取得最小值”.(说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.)
取得最小值”.(说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.)
(本题满分12分)
某简谐运动的图像对应的函数解析式为:![]() .
.
(1)指出此简谐运动的周期、振幅、频率、相位和初相;
(2)利用“五点法”作出函数在一个周期(闭区间)上的简图;
(3)说明它是由函数y=sinx的图像经过哪些变换而得到的。
【解】:(1)周期: ; 振幅: ;
频率: ; 相位: ;初相: ;
|
| |||||
| | 0 | ||||
|
| |||||
| |
(2)

(3)① 先将函数![]() 的图像 得到函数
的图像 得到函数
![]() 的图像;② 再将函数
的图像;② 再将函数![]() 的图像 得到
的图像 得到
函数![]() 的图像;③ 最后再将函数
的图像;③ 最后再将函数![]() 的图像
的图像
得到函数![]() 的图像。
的图像。
(本题满分18分,其中第1小题5分,第2小题5分,第3小题8分)
在平面直角坐标系中,已知 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,其中
,其中 且
且 .设
.设 .
.
(1)若 ,
, ,
, ,求方程
,求方程 在区间
在区间 内的解集;
内的解集;
(2)若点 是过点
是过点 且法向量为
且法向量为 的直线
的直线 上的动点.当
上的动点.当 时,设函数
时,设函数 的值域为集合
的值域为集合 ,不等式
,不等式 的解集为集合
的解集为集合 . 若
. 若 恒成立,求实数
恒成立,求实数 的最大值;
的最大值;
(3)根据本题条件我们可以知道,函数 的性质取决于变量
的性质取决于变量 、
、 和
和 的值. 当
的值. 当 时,试写出一个条件,使得函数
时,试写出一个条件,使得函数 满足“图像关于点
满足“图像关于点 对称,且在
对称,且在 处
处 取得最小值”.(说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.)
取得最小值”.(说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.)
(本题满分12分)为了了解某年段1000名学生的百米成绩情况,随机抽取了若
干学生的百米成绩,成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组
[13,14);第二组[14,15);……;第五组[17,18].按上述分组方法得到的频率分布直方图如
图所示,已知图中从左到右的前3个组的频率之比为3∶8∶19,且第二组的频数为8.
(1)将频率当作概率,请估计该年段学生中百米成绩在[16,17)内的人数;
(2)求调查中随机抽取了多少个学生的百米成绩;
(3)若从第一、五组中随机取出两个成绩,求这两个成绩的差的绝对值大于1秒的概率.

(本题满分12分)
某学校餐厅新推出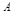 、
、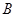 、
、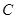 、
、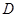 四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20分进行统计,统计结果如下面表格所示:[来源:学|科|网]
四款套餐,某一天四款套餐销售情况的条形图如下.为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20分进行统计,统计结果如下面表格所示:[来源:学|科|网]
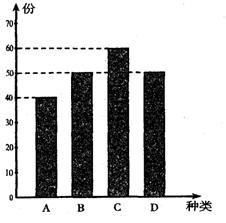
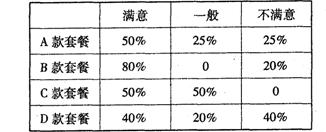
(1)
若同学甲选择的是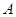 款套餐,求甲的调查问卷被选中的概率;
款套餐,求甲的调查问卷被选中的概率;
(2)
若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈,求这2人中至少有一人选择的是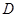 款套餐的概率。
款套餐的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com