练习册

  • 练习册
  • 试题
    即S的最大值为. 【查看更多】

     

    题目列表(包括答案和解析)

    （1）若直角三角形两直角边长之和为12，求其周长p的最小值；
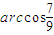    （2）若三角形有一个内角为，周长为定值p，求面积S的最大值；
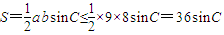    （3）为了研究边长a、b、c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值，现有解法如下：，要使S的值最大，则应使sinC最大，即使∠C最大，也就是使∠C所对的边c边长最大，所以，当a?9，b?8，c?4时该三角形面积最大，此时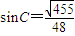，，所以，该三角形面积的最大值是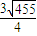．以上解答是否正确？若不正确，请你给出正确的解答．

    查看答案和解析>>

    （1）若直角三角形两直角边长之和为12，求其周长p的最小值；
    （2）若三角形有一个内角为arccos
    7
    9
    ，周长为定值p，求面积S的最大值；
    （3）为了研究边长a、b、c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值，现有解法如下：S=
    1
    2
    absinC≤
    1
    2
    ×9×8sinC=36sinC    ，要使S的值最大，则应使sinC最大，即使∠C最大，也就是使∠C所对的边c边长最大，所以，当a?9，b?8，c?4时该三角形面积最大，此时cosC=
    43
    48
    ，sinC=
    		455
    48
    ，所以，该三角形面积的最大值是
    3
    		455
    4
    ．以上解答是否正确？若不正确，请你给出正确的解答．

    查看答案和解析>>

    （2005•上海模拟）（1）若直角三角形两直角边长之和为12，求其周长p的最小值；
    （2）若三角形有一个内角为arccos
    7
    9
    ，周长为定值p，求面积S的最大值；
    （3）为了研究边长a、b、c满足9≥a≥8≥b≥4≥c≥3的三角形其面积是否存在最大值，现有解法如下：S=
    1
    2
    absinC≤
    1
    2
    ×9×8sinC=36sinC    ，要使S的值最大，则应使sinC最大，即使∠C最大，也就是使∠C所对的边c边长最大，所以，当a?9，b?8，c?4时该三角形面积最大，此时cosC=
    43
    48
    ，sinC=
    		455
    48
    ，所以，该三角形面积的最大值是
    3
    		455
    4
    ．以上解答是否正确？若不正确，请你给出正确的解答．

    查看答案和解析>>

         在某校组织的一次篮球定点投篮训练中，规定每人最多投3次；在A处每投进一球得3分，在B处每投进一球得2分；如果前两次得分之和超过3分即停止投篮，否则投第三次，某同学在A处的命中率q高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。为0.25，在B处的命中率为q高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。，该同学选择先在A处投一球，以后都在B处投，用高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。表示该同学投篮训练结束后所得的总分，其分布列为

      高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。          

    0          

    2             

       3   

       4   

       5   

    w.w.w.k.s.5.u.c.o.m       p        

    0.03          

       P1              

       P2         

    P3          

    P4              

    （1）      求q高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的值；w.w.w.k.s.5.u.c.o.m    

    （2）      求随机变量高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。的数学期望E高考资源网( www.ks5u.com)，中国最大的高考网站，您身边的高考专家。;

    （3）      试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。

    查看答案和解析>>

    在正四棱锥S—ABCD中，E是BC的中点，P点在侧面△SCD内及其边界上运动，并且总是保持PE⊥AC.

    （1）指出动点P的轨迹（即说明动点P在满足给定的条件下运动时所形成的图形），证明你的结论;

    （2）以轨迹上的动点P为顶点的三棱锥P－CDE的最大体积是正四棱锥S—ABCD体积的几分之几？

    （3）设动点P在G点的位置时三棱锥P－CDE的体积取最大值V1，二面角G—DE—C的大小为α，二面角G—CE—D的大小为β，求tanα∶tanβ的值；

    （4）若将“E是BC的中点”改为“E是BC上异于B、C的一定点”，其他条件不变，请指出点P的轨迹，证明你的结论.

    查看答案和解析>>


    同步练习册答案