
题目列表(包括答案和解析)
解:因为有负根,所以![]() 在y轴左侧有交点,因此
在y轴左侧有交点,因此![]()
解:因为函数没有零点,所以方程![]() 无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
无根,则函数y=x+|x-c|与y=2没有交点,由图可知c>2
13.证明:(1)令x=y=1,由已知可得f(1)=f(1×1)=f(1)f(1),所以f(1)=1或f(1)=0
若f(1)=0,f(0)=f(1×0)=f(1)f(0)=0,所以f(1)=f(0)与已知条件“![]() ”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
”矛盾所以f(1)≠0,因此f(1)=1,所以f(1)-1=0,1是函数y=f(x)-1的零点
(2)因为f(1)=f[(-1)×(-1)]=f2(-1)=,所以f(-1)=±1,但若f(-1)=1,则f(-1)=f(1)与已知矛盾所以f(-1)不能等于1,只能等于-1。所以任x∈R,f(-x)=f(-1)f(x)=-f(x),因此函数是奇函数
数字1,2,3,4恰好排成一排,如果数字i(i=1,2,3,4)恰好出现在第i个位置上则称有一个巧合,求巧合数![]() 的分布列。
的分布列。
已知椭圆
 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.
(I)求椭圆 的方程;
的方程;
(II)若过点 (2,0)的直线与椭圆
(2,0)的直线与椭圆 相交于两点
相交于两点 ,设
,设 为椭圆上一点,且满足
为椭圆上一点,且满足 (O为坐标原点),当
(O为坐标原点),当 <
< 时,求实数
时,求实数 的取值范围.
的取值范围.
【解析】本试题主要考查了椭圆的方程以及直线与椭圆的位置关系的运用。
第一问中,利用
第二问中,利用直线与椭圆联系,可知得到一元二次方程中 ,可得k的范围,然后利用向量的
,可得k的范围,然后利用向量的 <
< 不等式,表示得到t的范围。
不等式,表示得到t的范围。
解:(1)由题意知

如图,在三棱柱 中,
中, 侧面
侧面 ,
, 为棱
为棱 上异于
上异于 的一点,
的一点, ,已知
,已知 ,求:
,求:
(Ⅰ)异面直线 与
与 的距离;
的距离;
(Ⅱ)二面角 的平面角的正切值.
的平面角的正切值.
【解析】第一问中,利用建立空间直角坐标系
解:(I)以B为原点, 、
、 分别为Y,Z轴建立空间直角坐标系.由于,
分别为Y,Z轴建立空间直角坐标系.由于,

在三棱柱 中有
中有
 ,
,
设


又 侧面
侧面 ,故
,故 . 因此
. 因此 是异面直线
是异面直线 的公垂线,则
的公垂线,则 ,故异面直线
,故异面直线 的距离为1.
的距离为1.
(II)由已知有 故二面角
故二面角 的平面角
的平面角 的大小为向量
的大小为向量 与
与 的夹角.
的夹角.

假设关于某设备的使用年限x(年)和所支出的维修费y(万元)有如下统计资料:
| x | 2 | 3 | 4 | 5 | 6 |
| y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知,y对x呈线性相关关系.试求:
(1)线性回归方程;
(2)估计使用年限为10年时,维修费用约是多少?思路分析:本题考查线性回归方程的求法和利用线性回归方程求两变量间的关系.
解:(1)
| i | 1 | 2 | 3 | 4 | 5 |
| xi | 2 | 3 | 4 | 5 | 6 |
| yi | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
| xiyi | 4.4 | 11.4 | 22.0 | 32.5 | 42.0 |
|
| |||||
b= =1.23,
=1.23,
a=![]() -b
-b![]() =5-1.23×4=0.08.
=5-1.23×4=0.08.
所以,回归直线方程为![]() =1.23x+0.08.
=1.23x+0.08.
(2)当x=10时,![]() =1.23×10+0.08=12.38(万元),
=1.23×10+0.08=12.38(万元),
即估计使用10年时维修费约为12.38万元.
学校要用三辆车从北湖校区把教师接到文庙校区,已知从北湖校区到文庙校区有两条公路,汽车走公路①堵车的概率为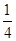 ,不堵车的概率为
,不堵车的概率为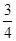 ;汽车走公路②堵车的概率为
;汽车走公路②堵车的概率为 ,不堵车的概率为
,不堵车的概率为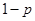 ,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为
,若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。(I)若三辆车中恰有一辆车被堵的概率为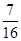 ,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数
,求走公路②堵车的概率;(Ⅱ)在(I)的条件下,求三辆车中被堵车辆的个数 的分布列和数学期望。
的分布列和数学期望。
【解析】第一问中,由已知条件结合n此独立重复试验的概率公式可知,得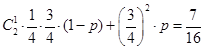
第二问中 可能的取值为0,1,2,3
可能的取值为0,1,2,3 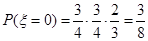 ,
, 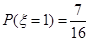
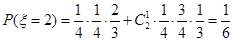 ,
,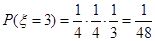
从而得到分布列和期望值
解:(I)由已知条件得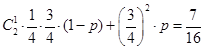 ,即
,即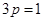 ,则
,则 的值为
的值为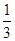 。
。
(Ⅱ) 可能的取值为0,1,2,3
可能的取值为0,1,2,3 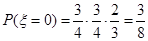 ,
, 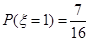
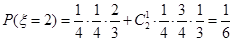 ,
,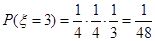
 的分布列为:(1分)
的分布列为:(1分)
|
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
所以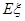
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com