
题目列表(包括答案和解析)
| |||||||||||||||
已知函数 在
在 处取得极值2.
处取得极值2.
⑴ 求函数 的解析式;
的解析式;
⑵ 若函数 在区间
在区间 上是单调函数,求实数m的取值范围;
上是单调函数,求实数m的取值范围;
【解析】第一问中利用导数
又f(x)在x=1处取得极值2,所以 ,
,
所以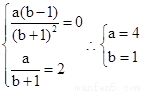
第二问中,
因为 ,又f(x)的定义域是R,所以由
,又f(x)的定义域是R,所以由 ,得-1<x<1,所以f(x)在[-1,1]上单调递增,在
,得-1<x<1,所以f(x)在[-1,1]上单调递增,在 上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有
上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有 ,得
,得
解:⑴ 求导 ,又f(x)在x=1处取得极值2,所以
,又f(x)在x=1处取得极值2,所以 ,即
,即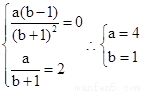 ,所以
,所以 …………6分
…………6分
⑵ 因为 ,又f(x)的定义域是R,所以由
,又f(x)的定义域是R,所以由 ,得-1<x<1,所以f(x)在[-1,1]上单调递增,在
,得-1<x<1,所以f(x)在[-1,1]上单调递增,在 上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有
上单调递减,当f(x)在区间(m,2m+1)上单调递增,则有 ,得
,得 , …………9分
, …………9分
当f(x)在区间(m,2m+1)上单调递减,则有
得 …………12分
…………12分
.综上所述,当 时,f(x)在(m,2m+1)上单调递增,当
时,f(x)在(m,2m+1)上单调递增,当 时,f(x)在(m,2m+1)上单调递减;则实数m的取值范围是
时,f(x)在(m,2m+1)上单调递减;则实数m的取值范围是 或
或
(本小题满分16分)通过研究学生的学习行为,心理学家发现,学生的接受能力依赖于老师引入概念和描述问题所用的时间:讲授开始时,学生的兴趣激增;中间有一段不太长的时间,学生的兴趣保持较理想的状态;随后学生的注意力开始分散.分析结果和实验表明,用f(x)表示学生掌握和接受概念的能力(f(x)的值越大,表示接受的能力越强),x表示提出和讲授概念的时间(单位:min),可有以下的公式:
(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
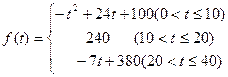
已知 ,且
,且 .
.
(1)求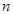 的值;
的值;
(2)求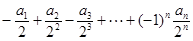 的值.
的值.
【解析】本试题主要考查了二项式定理的运用,以及系数求和的赋值思想的运用。第一问中,因为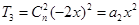 ,所以
,所以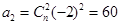 ,可得
,可得 ,第二问中,因为
,第二问中,因为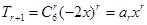 ,所以
,所以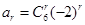 ,所以
,所以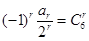 ,利用组合数性质可知。
,利用组合数性质可知。
解:(1)因为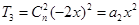 ,所以
,所以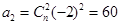 , ……3分
, ……3分
化简可得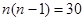 ,且
,且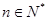 ,解得
,解得 . …………6分
. …………6分
(2)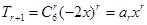 ,所以
,所以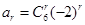 ,
,
所以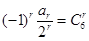 ,
,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com