题目列表(包括答案和解析)
（本小题满分12）已知等差数列{
}中，
求{}前n项和
.解析：本题考查等差数列的基本性质及求和公式运用能力，利用方程的思想可求解。
解：设
的公差为
，则
即
解得
因此
|
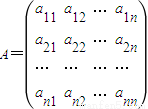，其中aik（1≤i≤n，1≤k≤n）表示该数阵中位于第i行第k列的数，已知该数阵每一行的数成等差数列，每一列的数成公比为2的等比数列，且a23=8，a34=20．
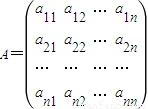，其中aik（1≤i≤n，1≤k≤n）表示该数阵中位于第i行第k列的数，已知该数阵每一行的数成等差数列，每一列的数成公比为2的等比数列，且a23=8，a34=20．已知等差数列{
}的公差为d（d
0），等比数列{
}的公比为q（q>1）。设
=
+
…..+ 
,
=-+…..+(-1
,n
(I) 若
=
= 1，d=2，q=3，求 
的值；
(II) 若=1，证明（1-q）
-（1+q）
=
，n；
(Ⅲ) 若正数n满足2
nq，设
的两个不同的排列， 
， 
证明
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com