
题目列表(包括答案和解析)
(本题13分)已知数列{an}中,a1 = t (t≠0,且t≠1),a2 = t2.且当x = t时,函数f (x) =![]() (an an 1)x2 (an + 1 an) x (n≥2)取得极值.
(an an 1)x2 (an + 1 an) x (n≥2)取得极值.
(1)求证:数列{an + 1 an}是等比数列;
(2)若bn = an ln |an| (n∈N+),求数列{bn}的前n项的和Sn;
(3)当t = ![]() 时,数列{bn}中是否存在最大项?如果存在,说明是第几项,如果不存在,请说明理由.
时,数列{bn}中是否存在最大项?如果存在,说明是第几项,如果不存在,请说明理由.
| 1 |
| 4 |
| 1 |
| 4 |
| a |
| b |
| a |
| b |
| π |
| 2 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 2 |
(本题满分13分) 探究函数![]() 的最大值,并确定取得最大值时
的最大值,并确定取得最大值时![]() 的值.列表如下:
的值.列表如下:
|
| … | -0.5 | -1 | -1.5 | -1.7 | -1.9 | -2 | -2.1 | -2.2 | -2.3 | -3 | … |
|
| … | -8.5 | -5 | -4.17 | -4.05 | -4.005 | -4 | -4.005 | -4.02 | -4.04 | -4.3 | … |
请观察表中![]() 值随
值随![]() 值变化的特点,完成以下的问题.
值变化的特点,完成以下的问题.
函数![]() 在区间
在区间![]() 上递减;
上递减;
(1)函数![]() 在区间 上递增.
在区间 上递增.
当![]() 时,
时,![]() .
.
(2)证明:函数![]() 在区间
在区间![]() 递减.
递减.
(3)思考:函数![]() 有最大值或最小值吗?如有,是多少?此时
有最大值或最小值吗?如有,是多少?此时![]() 为何值?(直接回答结果,不需证明).
为何值?(直接回答结果,不需证明).
(本题满分13分) 已知函数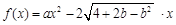 ,
,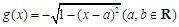 .
.
(1)当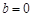 时,若
时,若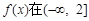 上单调递减,求a的取值范围;
上单调递减,求a的取值范围;
(2)求满足下列条件的所有整数对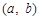 :存在
:存在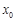 ,使得
,使得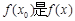 的最大值,
的最大值,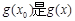 的最小值;
的最小值;
(本小题满分13分)
已知点 是函数
是函数 的图像上的两点,若对于任意实数
的图像上的两点,若对于任意实数 ,当
,当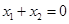 时,以
时,以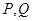 为切点分别作函数
为切点分别作函数 的图像的切线,则两切线必平行,并且当
的图像的切线,则两切线必平行,并且当 时函数
时函数 取得极小值1.[来源:]
取得极小值1.[来源:]
(1)求函数 的解析式;
的解析式;
(2)若 是函数
是函数 的图像上的一点,过
的图像上的一点,过 作函数
作函数 图像的切线,切线与
图像的切线,切线与 轴和直线
轴和直线 分别交于
分别交于 两点,直线
两点,直线 与
与 轴交于
轴交于 点,求△ABC的面积的最大值.
点,求△ABC的面积的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com