
题目列表(包括答案和解析)
(14分)已知直线L过抛物线x2=2py(p>0)的焦点F,且与抛物线交于A,B两点,Q是线段AB的中点,M是抛物线的准线与y轴的交点,0是坐标原点
(1)若直线L与x轴平行,且直线与抛物线所围区域的面积为6,求p的值.
(2)过A,B两点分别作该抛物线的切线,两切线相交于N点,求证:![]() ,
,![]()
(14分)已知函数![]() ,( x>0).
,( x>0).
(I)当0<a<b,且f(a)=f(b)时,求证:ab>1;
(II)是否存在实数a,b(a<b),使得函数y=f(x)的定义域、值域都是[a,b],若存在,则求出a,b的值,若不存在,请说明理由.
(III)若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [ma,mb]
(m≠0),求m的取值范围.
(14分)某养殖厂需定期购买饲料,已知该厂每天需要饲料200公斤,每公斤饲料的价格为1.8元,饲料的保管与其他费用为平均每公斤每天0.03元,购买饲料每次支付运费300元.
(Ⅰ)求该厂多少天购买一次饲料才能使平均每天支付的总费用最小;
(Ⅱ)若提供饲料的公司规定,当一次购买饲料不少5吨时其价格可享受八五折优惠(即原价的85%).问该厂是否考虑利用此优惠条件,请说明理由.
(14分) 如图,椭圆![]() 的右准线l交x轴于点M,AB为过焦点F的弦,且直线AB的倾斜角
的右准线l交x轴于点M,AB为过焦点F的弦,且直线AB的倾斜角![]()
![]() .
.
(Ⅰ)当![]() 的面积最大时,求直线AB的方程.
的面积最大时,求直线AB的方程.
(Ⅱ)()试用![]() 表示
表示![]() ;
;
()若![]() ,求直线AB的方程.
,求直线AB的方程.

. (14分)
某分公司经销某种品牌产品,每件产品的成本为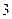 元,并且每件产品需向总公司交
元,并且每件产品需向总公司交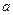 元(
元(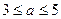 )的管理费,预计当每件产品的售价为
)的管理费,预计当每件产品的售价为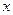 元(
元(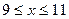 )时,一年的销售量为
)时,一年的销售量为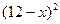 万件.
万件.
(1)求分公司一年的利润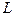 (万元)与每件产品的售价
(万元)与每件产品的售价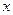 的函数关系式;
的函数关系式;
(2)当每件产品的售价为多少元时,分公司一年的利润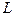 最大,并求出
最大,并求出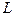 的最大值
的最大值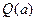 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com