
题目列表(包括答案和解析)
(文)(本小题8分)
如图,在四棱锥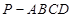 中,
中, 平面
平面 ,
, ,
, ,
,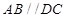 ,
,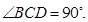
(1)求证: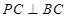 ;
;
(2)求点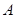 到平面
到平面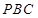 的距离
的距离
证明:(1) 平面
平面 ,
,
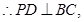 又
又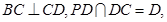
 平面
平面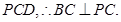 (4分)
(4分)
(2)设点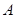 到平面
到平面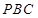 的距离为
的距离为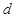 ,
,
 ,
, ,
,
求得 即点
即点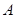 到平面
到平面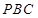 的距离为
的距离为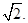 (8分)
(8分)
(其它方法可参照上述评分标准给分)
(本小题满分12分)如图,在直三棱柱 中,
中,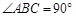 ,
,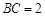 ,
, ,
, ,E在
,E在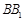 上,且
上,且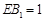 ,
,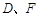 分别为
分别为 的中点.
的中点.
(1)求证: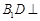 平面
平面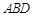 ;
;
(2)求异面直线 与
与 所成的角;
所成的角;
(3)求点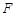 到平面
到平面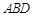 的距离.
的距离.

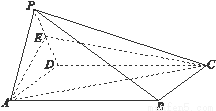
如图,四棱锥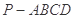 中,底面
中,底面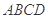 为正方形,
为正方形,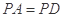
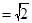 ,
,
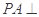 平面
平面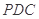 ,
,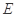 为棱
为棱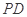 的中点.
的中点.
(1)求证:平面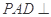 平面
平面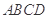 ;
;
(2)求二面角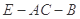 的余弦值.
的余弦值.
(3)求点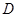 到平面
到平面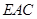 的距离.
的距离.
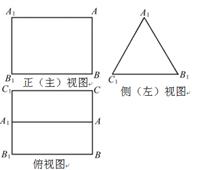
如图是三棱柱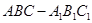 的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,
的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,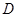 为
为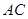 的中点.
的中点.
(1)求证: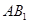 ∥平面
∥平面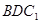 ;
;
(2)设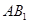 垂直于
垂直于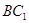 ,且
,且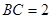 ,求点
,求点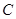 到平面
到平面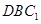 的距离.
的距离.
(08年安徽皖南八校联考)(本小题满分14分)
 如图所示,边长为2的等边△
如图所示,边长为2的等边△![]() 所在的平面垂直于矩形
所在的平面垂直于矩形![]() 所在的平面,
所在的平面,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)证明:![]() ⊥
⊥![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com