练习册

  • 练习册
  • 试题
    (Ⅱ)求以线段的中点为圆心且与直线相切的圆的方程． 【查看更多】

     

    题目列表(包括答案和解析)

    已知椭圆的中心在坐标原点O，焦点在x轴上，离心率为
    		2
    2
    ，坐标原点O到过右焦点F且斜率为1的直线的距离为
    		2
    2
    ．
    （1）求椭圆的方程；
    （2）设过右焦点F且与坐标轴不垂直的直线l交椭圆于P、Q两点，在线段OF上是否存在点M（m，0），使得以MP、MQ为邻边的平行四边形是菱形？若存在，求出m的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    已知椭圆的中心在坐标原点O，焦点在轴上，离心率为，坐标原点到过右焦点F且斜率为1的直线的距离为。

    （1）求椭圆的方程；

    （2）设过右焦点F且与坐标轴不垂直的直线交椭圆于P、Q两点，在线段上是否存在点,使得以为邻边的平行四边形是菱形？若存在，求出的取值范围；若不存在，请说明理由。

    查看答案和解析>>

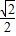    已知椭圆的中心在坐标原点O，焦点在x轴上，离心率为，坐标原点O到过右焦点F且斜率为1的直线的距离为．
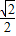    （1）求椭圆的方程；
    （2）设过右焦点F且与坐标轴不垂直的直线l交椭圆于P、Q两点，在线段OF上是否存在点M（m，0），使得以MP、MQ为邻边的平行四边形是菱形？若存在，求出m的取值范围；若不存在，请说明理由．

    查看答案和解析>>

    已知以动点P为圆心的圆与直线y=-
    1
    20
    相切，且与圆x2+（y-
    1
    4
    ）2=
    1
    25
    外切．
    （Ⅰ）求动P的轨迹C的方程；
    （Ⅱ）若M（m，m1），N（n，n1）是C上不同两点，且 m2+n2=1，m+n≠0，直线L是线段MN的垂直平分线．
        （1）求直线L斜率k的取值范围；
        （2）设椭圆E的方程为
    x2
    2
    +
    y2
    a
    =1（0＜a＜2）．已知直线L与抛物线C交于A、B两个不同点，L与椭圆E交于P、Q两个不同点，设AB中点为R，PQ中点为S，若
    OR
    •
    OS
    =0，求E离心率的范围．

    查看答案和解析>>

    已知直线l的方程为，且直线l与x轴交于点M，圆与x轴交于两点（如图）．

    （I）过M点的直线交圆于两点，且圆孤恰为圆周的，求直线的方程；

    （II）求以l为准线，中心在原点，且与圆O恰有两个公共点的椭圆方程；

    （III）过M点的圆的切线交（II）中的一个椭圆于两点，其中两点在x轴上方，求线段CD的长．

    查看答案和解析>>

    一、选择题（本大题共8小题，每小题5分，共40分）

    1.B   2. B   3. C   4. C   5.D   6. B   7.C   8. B.

     

    二、填空题（本大题共6小题，每小题5分，共30分）

    9. 6，17，28，39，40，51，62，73 .  10. .     11. 0. 

    12. 20.   13. .     14. .    15. .

    三、解答题（本大题共6小题，共80分）

    16.（本小题满分12分）

    解：（Ⅰ），即，

    ∴，∴．∵，∴．

    （Ⅱ）mn ，

    |mn|．

    ∵，∴，∴．从而．

    ∴当＝1，即时，|mn|取得最小值．

    所以，|mn|．

     

    17．（本小题满分12分）

    解：（1）设掷两颗正方体骰子所得的点数记为（x，y），其中，

    则获一等奖只有（6，6）一种可能，其概率为：；   

    获二等奖共有（6，5）、（5，6）、（4，6）、（6，4）、（5，5）共5种可能，其概率为：；

    设事件A表示“同行的三位会员一人获一等奖、两人获二等奖”，则有：

    P（A）=；                        

    ξ

    30-a

    -70

    0

    30

    p

    （2）设俱乐部在游戏环节收益为ξ元，则ξ的可能取值为,,0,,…7分

    其分布列为：

     

     

     

     

    则：Eξ=；

    由Eξ=0得：a=310，即一等奖可设价值为310 元的奖品。      

     

    18．（本小题满分14分）

    证明：（1）取EC的中点是F，连结BF，

    则BF//DE，∴∠FBA或其补角即为异面直线DE与AB所成的角．

    在△BAF中，AB=，BF=AF=．∴．

    ∴异面直线DE与AB所成的角的余弦值为．………5分

    （2）AC⊥平面BCE，过C作CG⊥DE交DE于G，连AG．

    可得DE⊥平面ACG，从而AG⊥DE

    ∴∠AGC为二面角A-ED-B的平面角．

    在△ACG中，∠ACG=90°，AC=4，ＣG=

    ∴．∴．

    ∴二面角A-ED-B的的正弦值为．

    （3）

    ∴几何体的体积V为16．

     

    方法二：（坐标法）（1）以C为原点，以CA，CB，CE所在直线为x,y,z轴建立空间直角坐标系．

    则A（4，0，0），B（0，4，0），D（0，4，2），E（0，0，4）

    ，∴

    ∴异面直线DE与AB所成的角的余弦值为．

    （2）平面BDE的一个法向量为，

    设平面ADE的一个法向量为，
    ∴

    从而,

    令，则,

    ∴二面角A-ED-B的的正弦值为．

    （3），∴几何体的体积V为16．

     

    19．（本小题满分14分）

    【解】（Ⅰ）法1：依题意，显然的斜率存在,可设直线的方程为，

    整理得 ． ①   

        设是方程①的两个不同的根，

        ∴，   ②                 

        且，由是线段的中点，得

        ，∴．

        解得，代入②得，的取值范围是（12，+∞）．

        于是，直线的方程为，即     

        法2：设，，则有

            

        依题意，，∴．              

    ∵是的中点，

    ∴，，从而．

    又由在椭圆内，∴，

    ∴的取值范围是．                          

    直线的方程为，即．       

    （Ⅱ）∵垂直平分，∴直线的方程为，即，

    代入椭圆方程，整理得．  ③         

    又设，的中点为，则是方程③的两根，

    ∴．

    到直线的距离，故所求的以线段的中点为圆心且与直线相切的圆的方程为：．

    20．（本小题满分14分）

    （Ⅰ）解：由题意得,,所以=

    （Ⅱ）证:令,,则=1

    所以=（1）,=（2）,

    （2）―（1）,得―=,

    化简得（3）

    （4）,（4）―（3）得

    在（3）中令,得,从而为等差数列

    （Ⅲ）记,公差为,则=

    则,

    则,当且仅当,即时等号成立

     

    21．（本小题满分14分）

    解：（1）由题意，≥0在上恒成立，即．

             ∵θ∈（0，π），∴．故在上恒成立，

             只须，即，只有．结合θ∈（0，π），得．

    （2）由（1），得．．

    ∵在其定义域内为单调函数，

    ∴或者在[1，＋∞）恒成立．

     等价于，即，

         而 ，（）max=1，∴．

    等价于，即在[1，＋∞）恒成立，

    而∈（0，1]，．

    综上，m的取值范围是．

    （3）构造，．

    当时，，，，所以在[1，e]上不存在一个，使得成立．

    当时，．

    因为，所以，，所以在恒成立．

    故在上单调递增，，只要，

    解得．故的取值范围是．

     

     


    同步练习册答案