
题目列表(包括答案和解析)
函数 在同一个周期内,当
在同一个周期内,当 时,
时, 取最大值1,当
取最大值1,当 时,
时, 取最小值
取最小值 。
。
(1)求函数的解析式
(2)函数 的图象经过怎样的变换可得到
的图象经过怎样的变换可得到 的图象?
的图象?
(3)若函数 满足方程
满足方程 求在
求在 内的所有实数根之和.
内的所有实数根之和.
【解析】第一问中利用
又因
又
 函数
函数
第二问中,利用 的图象向右平移
的图象向右平移 个单位得
个单位得 的图象
的图象
再由 图象上所有点的横坐标变为原来的
图象上所有点的横坐标变为原来的 .纵坐标不变,得到
.纵坐标不变,得到 的图象,
的图象,
第三问中,利用三角函数的对称性, 的周期为
的周期为
 在
在 内恰有3个周期,
内恰有3个周期,
并且方程 在
在 内有6个实根且
内有6个实根且
同理, 可得结论。
可得结论。
解:(1)
又因
又
 函数
函数
(2) 的图象向右平移
的图象向右平移 个单位得
个单位得 的图象
的图象
再由 图象上所有点的横坐标变为原来的
图象上所有点的横坐标变为原来的 .纵坐标不变,得到
.纵坐标不变,得到 的图象,
的图象,
(3) 的周期为
的周期为
 在
在 内恰有3个周期,
内恰有3个周期,
并且方程 在
在 内有6个实根且
内有6个实根且
同理,
故所有实数之和为
命题P:![]() cn=0.
cn=0.
命题Q:当x∈[![]() ,2]时,函数f(x)=x+
,2]时,函数f(x)=x+![]() >
>![]() 恒成立.
恒成立.
如果P或Q为真命题,P且Q为假命题,求c的取值范围.
分析:由![]() cn=0得,0<c<1.∴P:0<c<1,
cn=0得,0<c<1.∴P:0<c<1,
由x∈[![]() ,2]时,函数f(x)=x+
,2]时,函数f(x)=x+![]() >
>![]() 恒成立,想到
恒成立,想到![]() <f(x)min,故需求f(x)在[
<f(x)min,故需求f(x)在[![]() ,2]上的最小值.
,2]上的最小值.
已知函数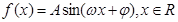 (其中
(其中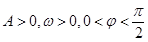 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为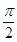 ,且图象上一个最低点为
,且图象上一个最低点为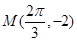 .
.
(1)求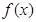 的解析式; (2)当
的解析式; (2)当 ,求
,求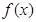 的值域.
的值域.
【解析】第一问利用三角函数的性质得到)由最低点为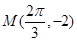 得A=2. 由x轴上相邻的两个交点之间的距离为
得A=2. 由x轴上相邻的两个交点之间的距离为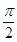 得
得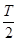 =
=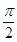 ,即
,即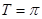 ,
,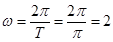 由点
由点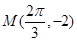 在图像上的
在图像上的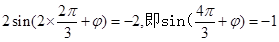
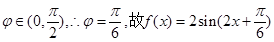
第二问中,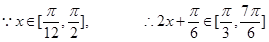

当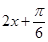 =
=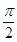 ,即
,即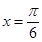 时,
时,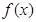 取得最大值2;当
取得最大值2;当
即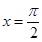 时,
时,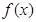 取得最小值-1,故
取得最小值-1,故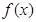 的值域为[-1,2]
的值域为[-1,2]
(本小题满分12分)已知f (x)=(1+x)m+(1+2x)n(m,n∈N*)的展开式中x的系数为11.
(1)求x2的系数的最小值;
(2)当x2的系数取得最小值时,求f (x)展开式中x的奇次幂项的系数之和.
解: (1)由已知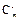 +2
+2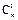 =11,∴m+2n=11,x2的系数为
=11,∴m+2n=11,x2的系数为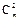 +22
+22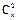 =
=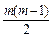 +2n(n-1)=
+2n(n-1)=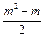 +(11-m)(
+(11-m)(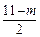 -1)=(m-
-1)=(m-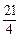 )2+
)2+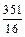 .
.
∵m∈N*,∴m=5时,x2的系数取最小值22,此时n=3.
(2)由(1)知,当x2的系数取得最小值时,m=5,n=3,
∴f (x)=(1+x)5+(1+2x)3.设这时f (x)的展开式为f (x)=a0+a1x+a2x2+…+a5x5,
令x=1,a0+a1+a2+a3+a4+a5=25+ 33,
33,
令x=-1,a0-a1+a2-a3+a4-a5=-1,
两式相减得2(a1+a3+a5)=60, 故展开式中x的奇次幂项的系数之和为30.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com