
题目列表(包括答案和解析)
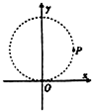 如图所示,在平面直角坐标系xoy中,以(O,R)为圆心,半径为R的圈形区城内有相互垂直的匀强电场和匀强磁场,磁感应强度B,方向垂直于xOy平面向里一带正电粒子从O点沿y轴正方向以v0入射进场区.恰好做匀速直线运动.不计宜重力作用
如图所示,在平面直角坐标系xoy中,以(O,R)为圆心,半径为R的圈形区城内有相互垂直的匀强电场和匀强磁场,磁感应强度B,方向垂直于xOy平面向里一带正电粒子从O点沿y轴正方向以v0入射进场区.恰好做匀速直线运动.不计宜重力作用| q | m |
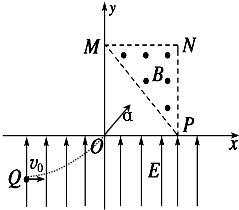 如图所示,在平面直角坐标系xOy内,第Ⅰ象限的等腰直角三角形MNP区域内存在垂直于坐标平面向外的匀强磁场,y<0的区域内存在着沿y轴正方向的匀强电场.一质量为m、电荷量为q的带正电粒子从电场中Q(-2h,-h)点以速度v0水平向右射出,经坐标原点O处射入第Ⅰ象限,最后以垂直于PN的方向射出磁场.已知MN平行于x轴,N点的坐标为(2h,2h),不计粒子的重力,求:
如图所示,在平面直角坐标系xOy内,第Ⅰ象限的等腰直角三角形MNP区域内存在垂直于坐标平面向外的匀强磁场,y<0的区域内存在着沿y轴正方向的匀强电场.一质量为m、电荷量为q的带正电粒子从电场中Q(-2h,-h)点以速度v0水平向右射出,经坐标原点O处射入第Ⅰ象限,最后以垂直于PN的方向射出磁场.已知MN平行于x轴,N点的坐标为(2h,2h),不计粒子的重力,求:如图所示,在平面直角坐标系xOy平面内,有以(![]() ,0)为圆心、半径为
,0)为圆心、半径为![]() 的圆形匀强磁场区域,磁场的磁感应强度大小为B,方向垂直于xOy平面向里。在
的圆形匀强磁场区域,磁场的磁感应强度大小为B,方向垂直于xOy平面向里。在![]() 的上方足够大的范围内,有沿x轴负方向的匀强电场,电场强度的大小为
的上方足够大的范围内,有沿x轴负方向的匀强电场,电场强度的大小为![]() 。从
。从![]() 点向偏右的不同方向发射速度大小相同的质子,质子的运动轨迹均在xOy平面内。已知质子在磁场中运动的轨道半径也为
点向偏右的不同方向发射速度大小相同的质子,质子的运动轨迹均在xOy平面内。已知质子在磁场中运动的轨道半径也为![]() ,质子的电荷量为
,质子的电荷量为![]() ,质量为
,质量为![]() ,不计质子的重力及所受的阻力。
,不计质子的重力及所受的阻力。
(1)求质子射入磁场时的速度大小。
(2)若质子的速度方向与x轴正方向成θ =30°角(如图所示)射入磁场,试求该质子到达y轴的位置。

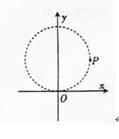
如图所示,在平面直角坐标系xoy中,以(0,R)为圆心,半径为R的圈形区城内有相互垂直的匀强电场和匀强磁场,磁感应强度B方向垂直于xOy平面向里,一带正电粒子从O点沿y轴正方向以v0入射进场区.恰好做匀速直线运![]() 动.不计重力作用。
动.不计重力作用。
(1)求电场强度E的大小和方向.
(2)若仅仅撤去磁场.带电位子仍从O点以相同的速度v0射入,经电场区的最右侧的P点射出,求粒子比荷q/m。
(3)若仅仅撤去电场.带电粒子仍从O点沿y轴正方向入射.但速度大小为2v0,求粒子在磁场中的运![]() 动时间.
动时间.
如图所示,在平面直角坐标系xoy内,第I象限的等腰直角三角形MNP区域内存在垂直于坐标平面向外的匀强磁场,y<0的区域内存在着沿y轴正方向的匀强电场。一质量为m、电荷量为q的带电粒子从电场中Q(-2h,-h)点以速度υ0水平向右射出,经坐标原点O处射入第I象限,最后以垂直于PN的方向射出磁场。已知MN平行于x轴, N点的坐标为(2h,2h),不计粒子的重力,求:
(1)电场强度的大小E;
(2)磁感应强度的大小B;
(3)粒子磁场中运动的时间t.
一、选择题(40分)
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
A
C
A
AD
D
ABD
BD
A
二、实验题
11.实物连线(6分)
12.(每空3分,共12分)(1)b D
(2)

三、计算题
13.(8分) 解:对导体棒受力分析
由欧姆定律得: (1)
(1)
导休棒所受安培力:
对导体棒由平衡物体得
解得: (3)
(3)
由牛顿第三定律可知,导体棒对轨导的动力为
 (1)
(1)
14.(10分)解:(1)路端电压
当 时,
时,
对闭合电路由
当 解得
解得
(2)当滑动触头左A端时

当滑动触头左B端y

所以当截时电场输出范围为0-11V
(3)当CD间电阻与滑动变阻器并联时电阻最小


而 解得
解得
15.(12分)解:直线 是磁场区域圆周的,而
是磁场区域圆周的,而 ,所以弦
,所以弦 是圆形磁场的直径,圆心为直径AB的中点O,直线
是圆形磁场的直径,圆心为直径AB的中点O,直线 也是带电粒子同的轨迹的各弦,且圆心是Y轴上的
也是带电粒子同的轨迹的各弦,且圆心是Y轴上的 点,由于数偏角为
点,由于数偏角为 ,则圆心角
,则圆心角 ,所以
,所以 是等边三角形。
是等边三角形。
(1)由所知识得:ab=IL w.w.w.k.s.5 u.c.o.m



(2)圆心 的横坐标
的横坐标
圆心 的纵坐标
的纵坐标
(3)带电粒子磁场中的运动时间

16.(12分)解:设物块与小车共同运动达最大数
对物块与小车由动量守恒定律得:

解得:
 而
而 ,因此物块与小车没有共速就离开小车
,因此物块与小车没有共速就离开小车
使物块离开小车最大数度

 (4)
(4)
(2)物块与小车分离时,小车速度最小为
对物块小车
由动量守恒定律得: 
解得
(3)由能量守恒定律知:系统机械能的减少等于内能的增加


www.ks5u.com
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com