题目列表(包括答案和解析)
log(
)(
)的值为( )?
A．1 B．0? C．－1 D．随t的变化而变化
)(
)的值为( )?
A．1 B．0? C．－1 D．随t的变化而变化
若f(x)=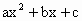
(a＜0)对于任意的t∈R，总有f(3＋t)=f(1－t)，那么
[ ]
若A，B，C是上不共线的三点，动点P满足
＝
[(1－t)
＋(1－t)
＋(1＋2t)
](t∈R且t≠0)，则点P的轨迹一定通过△ABC的
A．内心
B．垂心
C．外心
D．AB边的中点
已知曲线C的方程是(t＋1)
＋2at)x＋3at＋b＝0，直线l的
方程是y＝t(x－1)，若对任意实数t，曲线C恒过定点P(1，0)．
(1)求定值a，b；
(2)直线l截曲线C所得弦长为d，记f(t)＝
，则当t为何值时，f(t)有最大值，最大值是多少？
(3)若点M(
)在曲线C上，又在直线l上，求
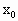的取值范围．
一、选择题：
（1）D （2）B （3）C （4）B （5）B （6）A
（7）C （8）A （9）D （10）B （11）C （12）B
二、填空题：
（13）2
（14）
（15）200 （16）②③
三、解答题
17.
(1)
故函数的定义域是(－1,1). ………… 2分
(2)由
,得
(
R),所以
, …………… 5分
所求反函数为
(
R).
………………… 7分
(3) 
=
=－
,所以是奇函数.……… 12分
18. (1)设
,则
.
………………… 1分
由题设可得
即
解得
………………… 5分
所以
.
………………… 6分
(2) 
,
. …… 8分
列表:
－
＋
－
＋
………………… 11分
由表可得:函数的单调递增区间为,
……………… 12分
19.（1）证明：设
，且
，
则
，且
.
………………… 2分
∵
在
上是增函数，∴
.
………………… 4分
又为奇函数，∴
,
∴
, 即在
上也是增函数.
……………… 6分
（2）∵函数在和上是增函数，且在R上是奇函数，
∴在
上是增函数.
…………………… 7分
于是
.
………… 10分
∵当
时，
的最大值为
，
∴当
时，不等式恒成立.
……………… 12分
20. ∵AB=x, ∴AD=12－x. ………………1分
又
，于是
.
………………3分
由勾股定理得 
整理得
…………5分
因此
的面积 
. ……7分
由
得
………………8分
∴
∴
.
………………10分
当且仅当
时，即当
时，S有最大值
……11分
答：当时，的面积有最大值
………………12分
21. (1) h (x)
…………………5分
(2) 当x≠1时, h(x)=
=x－1+
+2,
………………6分
若 x > 1时, 则 h (x)≥4,其中等号当 x = 2时成立 ………………8分
若x<1时, 则h (x) ≤ 0,其中等号当 x = 0时成立 ………………10分
∴函数 h (x)的值域是 (－∞,0 ] ∪ { 1 } ∪ [ 4 ,＋∞) ………………12分
22. （1）
切线PQ的方程
………2分
（2）令y=0得
………4分
由
解得 
.
………6分
又0<t<6, ∴4<t<6， ………7分
g (t)在(m, n)上单调递减，故（m, n）
………8分
（3）当
在（0，4）上单调递增，
∴P的横坐标的取值范围为
.
………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com