
题目列表(包括答案和解析)
C.选修4-4:坐标系与参数方程
在极坐标系下,已知圆O: 和直线
和直线 ,
,
(1)求圆O和直线 的直角坐标方程;(2)当
的直角坐标方程;(2)当 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.
D.选修4-5:不等式证明选讲
对于任意实数
 和
和 ,不等式
,不等式 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围.
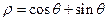 和直线
和直线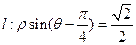 ,
, 的直角坐标方程;(2)当
的直角坐标方程;(2)当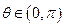 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.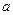
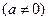 和
和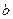 ,不等式
,不等式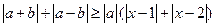 恒成立,试求实数
恒成立,试求实数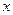 的取值范围.
的取值范围.| 3 |
| 3 |
.本小题满分15分)
如图,已知椭圆E: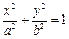
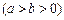 ,焦点为
,焦点为 、
、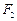 ,双曲线G:
,双曲线G: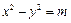
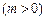 的顶点是该椭
的顶点是该椭 圆的焦点,设
圆的焦点,设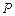 是双曲线G上异于顶点的任一点,直线
是双曲线G上异于顶点的任一点,直线 、
、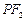 与椭圆的交点分别为A、B和C、D,已知三角形
与椭圆的交点分别为A、B和C、D,已知三角形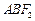 的周长等于
的周长等于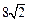 ,椭圆四个顶点组成的菱形的面积为
,椭圆四个顶点组成的菱形的面积为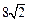 .
.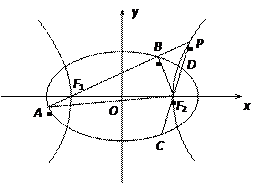
(1)求椭圆E与双曲线G的方程;
(2)设直线 、
、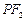 的斜率分别为
的斜率分别为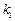 和
和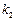 ,探求
,探求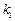 和
和
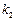 的关系;
的关系;
(3)是否存在常数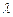 ,使得
,使得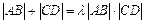 恒成立?
恒成立?
若存在,试求出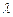 的值;若不存在, 请说明理由.
的值;若不存在, 请说明理由.
一、选择题(每小题5分,共40分)
题号
1
2
3
4
5
6
7
8
答案
A
A
C
D
C
A
B
D
二、填空题(每小题5分,共30分)
9.84; 10. ; 11.45; 12. -6; 13.
; 11.45; 12. -6; 13. ; 14.
; 14. ; 15.3
; 15.3
三、解答题(共80分.解答题应写出推理、演算步骤)
16. 解:(1)
则 的最小正周期
的最小正周期 , ……………………………4分
, ……………………………4分
且当 时
时 单调递增.
单调递增.
即 为
为 的单调递增区间(写成开区间不
的单调递增区间(写成开区间不
扣分).…………6分
(2)当 时
时 ,
,
当 ,即
,即 时
时 .
.
所以 . ……………9分
. ……………9分
 为
为 的对称轴. ……12分
的对称轴. ……12分
17. 解:(1)依题意, 的可能取值为1,0,-1
………1分
的可能取值为1,0,-1
………1分
 的分布列为
…4分
的分布列为
…4分

1
0

p



 =
=
 =
= …………6分
…………6分
(2)设 表示10万元投资乙项目的收益,则
表示10万元投资乙项目的收益,则 的分布列为……8分
的分布列为……8分

2




 …………10分
…………10分
依题意要求 … 11分
… 11分
∴ ………12分
………12分
注:只写出 扣1分
扣1分
18. 解:(1)①当直线 垂直于
垂直于 轴时,则此时直线方程为
轴时,则此时直线方程为 ,
, 与圆的两个交点坐标为
与圆的两个交点坐标为 和
和 ,其距离为
,其距离为 满足题意 ………1分
满足题意 ………1分
②若直线 不垂直于
不垂直于 轴,设其方程为
轴,设其方程为 ,即
,即
设圆心到此直线的距离为 ,则
,则 ,得
,得 …………3分
…………3分
∴ ,
, ,
,
故所求直线方程为
综上所述,所求直线为 或
或 …………7分
…………7分
(2)设点 的坐标为
的坐标为 (
( ),
), 点坐标为
点坐标为
则 点坐标是
点坐标是 …………9分
…………9分
∵ ,
,
∴ 即
即 ,
,
 …………11分
…………11分
又∵ ,∴
,∴
∴ 点的轨迹方程是
点的轨迹方程是 ,
…………13分
,
…………13分
轨迹是一个焦点在 轴上的椭圆,除去短轴端点。 …………14分
轴上的椭圆,除去短轴端点。 …………14分
19.解一:(1)证明:连结AD1,由长方体的性质可知:
 AE⊥平面AD1,∴AD1是ED1在
AE⊥平面AD1,∴AD1是ED1在
平面AD1内的射影。又∵AD=AA1=1,
∴AD1⊥A1D
∴D1E⊥A1D1(三垂线定理) 4分
(2)设AB=x,∵四边形ADD1A是正方形,
∴小蚂蚁从点A沿长方体的表面爬到
 点C1可能有两种途径,如图甲的最短路程为
点C1可能有两种途径,如图甲的最短路程为

如图乙的最短路程为



 ………………9分
………………9分
(3)假设存在,平面DEC的法向量 ,
,
设平面D1EC的法向量 ,则
,则
 …………………12分
…………………12分
由题意得:
解得: (舍去)
(舍去)
 ………14分
………14分
20. 解:(1)当 .…(1分)
.…(1分)
 ……(3分)
……(3分)
∴ 的单调递增区间为(0,1),单调递减区间为:
的单调递增区间为(0,1),单调递减区间为: ,
, .
.
……(4分)
(2)切线的斜率为 ,
,
∴ 切线方程为 .……(6分)
.……(6分)
所求封闭图形面积为
 .
.
……(8分)
(3) , ……(9分)
, ……(9分)
令 .
……(10分)
.
……(10分)
列表如下:
x
(-∞,0)
0
(0,2-a)
2-a
(2-a,+ ∞)

-
0
+
0
-

ㄋ
极小
ㄊ
极大
ㄋ
由表可知, .
……(12分)
.
……(12分)
设 ,
,
∴ 上是增函数,……(13分)
上是增函数,……(13分)
∴
 ,即
,即 ,
,
∴不存在实数a,使 极大值为3.
……(14)
极大值为3.
……(14)
21.解:(1)由 而
而
 解得A=1……………………………………2分
解得A=1……………………………………2分
(2)令

当n=1时,a1=S1=2,当n≥2时,an=Sn-Sn-1=n2+n
综合之:an=2n…………………………………………6分
由题意
∴数列{cn+1}是 为公比,以
为公比,以 为首项的等比数列。
为首项的等比数列。
 ………………………9分
………………………9分
(3)当

 ………………………11分
………………………11分
当
 ………13分
………13分
综合之:
………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com