
题目列表(包括答案和解析)
已知椭圆的中心为坐标原点,短轴长为2,一条准线方程为l:x=2.
(1)求椭圆的标准方程;
(2)设O为坐标原点,F是椭圆的右焦点,点M是直线l上的动点,过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值.
已知椭圆的中心为坐标原点,短轴长为2,一条准线方程为l:x=2.
(1)求椭圆的标准方程;
(2)设O为坐标原点,F是椭圆的右焦点,点M是直线l上的动点,过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值.
已知椭圆的中心为坐标原点O,椭圆短轴长为2,动点![]()
![]() 在椭圆的准线上。
在椭圆的准线上。
(1)求椭圆的标准方程;
(2)求以OM为直径且被直线![]() 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程;
(3)设F是椭圆的右焦点,过点F作OM的垂线与以OM为直径的圆交于点N,求证:线段ON的长为定值,并求出这个定值。
已知椭圆的中心为坐标原点O,焦点在![]() 轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,
轴上,斜率为1且过椭圆右焦点F的直线交椭圆于A、B两点,![]() 与
与![]() 共线
共线![]()
(Ⅰ)求椭圆的离心率;
(Ⅱ)设M为椭圆上任意一点,且![]() ,证明
,证明![]() 为定值
为定值![]()
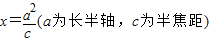 上.
上.一. 每小题5分,共60分 DACDB DACBB DD
二. 每小题5分,共20分.其中第16题前空2分,后空3分.
13.
60;
14.  ; 15.
; 15.  ; 16. 2,-
; 16. 2,-
三.解答题:本大题共6个小题,共70分.解答应写出文字说明,证明过程或演算步骤.
17.(Ⅰ)
∴


(Ⅱ) (7分)
(7分)
 (8分)
(8分)
∴ (10分)
(10分)
18.解:(Ⅰ)记“该人被录用”的事件为事件A,其对立事件为 ,则
,则


(Ⅱ)该生参加测试次数ξ的可能取值为2,3,4,依题意得
|