
题目列表(包括答案和解析)
|
| 1 |
| x+1 |


|
|
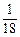 x2-
x2-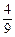 x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)
x-10与x轴的交点为A,与y轴的交点为点B,过点B作x轴的平行线BC,交抛物线于点C,连结AC.现有两动点P,Q分别从O,C两点同时出发,点P以每秒4个单位的速度沿OA向终点A移动,点Q以每秒1个单位的速度沿CB向点B移动,点P停止运动时,点Q也同时停止运动.线段OC,PQ相交于点D,过点D作DE∥OA,交CA于点E,射线QE交x轴于点F.设动点P,Q移动的时间为t(单位:秒)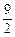 )时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;
)时,△PQF的面积是否总为定值?若是,求出此定值;若不是,请说明理由;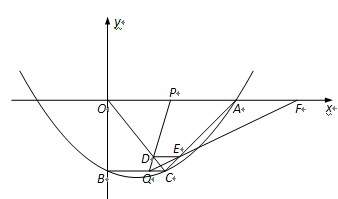
市场营销人员对过去几年某商品的价格及销售数量的关系作数据分析发现有如下规律:该商品的价格每上涨x%(x>0),销售数量就减少kx%(其中k为正常数),目前该商品定价为每个a元,统计其销售数量为b个.
(1)k=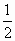 时,该商品的价格上涨多少,就能使销售的总金额达到最大?
时,该商品的价格上涨多少,就能使销售的总金额达到最大?
(2)在适当的涨价过程中,求使销售总金额不断增加时k的取值范围.
如图:A、B是两个定点,且|AB|=2,动点M到A点的距离是4,线段MB的垂直平分线l交MA于点P,直线k垂直于直线AB,且B点到直线k的距离为3.
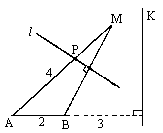
(Ⅰ)建立适当的坐标系,求动点P的轨迹方程;
(Ⅱ)求证:点P到点B的距离与点P到直线k的距离之比为定值;
(Ⅲ)(理)若点P到A、B两点的距离之积为m,当m取最大值时,求P点的坐标.
通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设f(x)表示学生注意力随时间t(分钟)的变化规律(f(t)越大,表明学生注意力越集中),经过实验分析得知:
f(t)=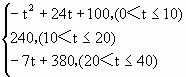
(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com