如图a所示，是利用重物自由下落验证机械能守恒定律的实验．
（1）某同学的实验操作步骤如下：
A．用天平测量出重锤的质量
B．按图示的装置安装器件
C．将打点计时器接到电源的直流输出端上
D．接通电源后释放纸带，打出一条纸带
E．换用另外的纸带，重复步骤D
F．选取合适的纸带
G．测量所选纸带上某些点之间的距离
H．根据测量的结果计算重锤下落过程中减少的重力势能和它增加的动能，比较二者是否相等
请你指出：①以上实验步骤中一个可以不必要的操作步骤是；②操作有错误的实验步骤是．（填字母代号）
（2）某实验小组打出了三条纸带，但是由于实验操作不规范，三条打点纸带的第1个点和第2个点之间的距离都明显的不接近2mm，于是他们选择了如图b所示的一条点迹清晰且在一条直线上的纸带进行数据处理．他们首先在所选择纸带的前四个点的上
方标上1、2、3、4，在后面适当的位置又选取了5个连续点，分别标上A、B、C、D、E；然后他们设计了三种数据处理方案来验证机械能守恒定律．

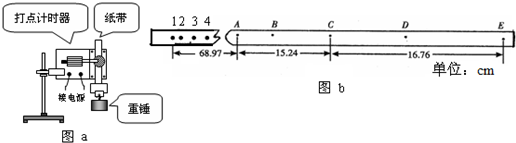
方案1：选择第1个点作为过程的起点，分别选择点B、C、D作为过程的终点，用刻度尺量出点A、B、C、D、E到第1个点的距离h₁、h₂、h₃、h₄、h₅，利用vn=

hn+1-hn-1

2T

算出重锤运动到点B、C、D时的速度，比较“mgh_n和

1

2

m

v

2 n

”是否相等来验证机械能是否守恒．
方案2：选择第3个点作为过程的起点，分别选择点B、C、D作为过程的终点，用刻度尺量出点A、B、C、D、E到第3个点的距离h₁、h₂、h₃、h₄、h₅，再数出点B、C、D到第3个点的时间间隔数k，利用v_n=gkT算出重锤运动到点B、C、D时的速度，利用v₃=2gT求出打第3个点时重锤的速度，比较“mgh_n和（

1

2

m

v

2 n

-

1

2

m

v

2 3

）”是否相等来验证机械能是否守恒．
方案3：选择第3个点作为过程的起点，分别选择点B、C、D作为过程的终点，用刻度尺量出点A、B、C、D、E到第3个点的距离h₁、h₂、h₃、h₄、h₅，利用

v

n

=

hn+1-hn-1

2T

算出重锤运动到点B、C、D时的速度，再测出第2个点到第4个点之间的距离S，利用v3=

S

2T

求出打第3个点时重锤的速度，比较“mgh_n和（

1

2

m

v

2 n

-

1

2

m

v

2 3

）”是否相等来验证机械能是否守恒．
①你认为最合理的实验方案是方案．
②你判断的理由是：．
③利用你选择的数据处理方案，可求得D点对应的速度为v_D=m/s（保留三位有效数字）．

银导线的横截面积4mm²，通过2A的电流，若每个银原子提供一个自由电子，则银导线1m长度上的自由电子数最接近下列哪一值（已知银的密度为10.5×10³Kg/m³，摩尔质量为0.108kg/mol）（　　）

“海宝”是2010年上海世博会的吉祥物，如图所示．点缀在上海街头的各种“海宝”中，有一座是材质均匀、实心的，其质量为3.0×10³kg，密度为1.5×10³kg/m³，与水平地面的接触面积为1m²，g取10N/kg，则（　　）

（2008?汕头二模）已知金刚石的密度为3.5×10³kg/m³，在体积为5.7×10^-8m³小块金刚石中，含有多少个炭原子？设金刚石中炭原子是紧密地排列在一起的，估算炭原子体积的大小．已知阿伏加德罗常数NA=6.0×1023mol-1．

1789年英国著名物理学家卡文迪许首先估算出了地球的平均密度．已知地球半径R=6400km，万有引力常量G=6.67×10^-11N?m²/kg²，根据你所学过的知识，估算出地球密度的大小最接近（　　）