
题目列表(包括答案和解析)
(08年雅礼中学二模文)雅礼中学高三文四同学积极参加向汶川地震灾区的捐款活动.现通过简单随机抽样的方法,抽取了其中20名同学进行统计:捐款100元的有4人,捐款200元的有10人,捐款300元的有6人。请用所学知识解答下列问题:
(I)从文四班这20名同学中任选三人,至少有一人捐款300元的概率是多少?
(II)从文四班这20名同学中任选三人,三人捐款之和不少于600元的概率是多少?
某中学号召本校学生在本学期参加市创办卫生城的相关活动,学校团委对该校学生是否关心创卫活动用简单抽样方法调查了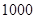 位学生(关心与不关心的各一半),
位学生(关心与不关心的各一半),
结果用二维等高条形图表示,如图.
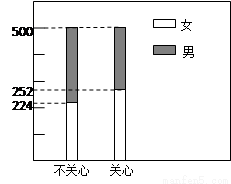
(1)完成列联表,并判断能否有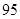 ℅的把握认为是否关心创卫活动与性别有关?
℅的把握认为是否关心创卫活动与性别有关?
|
|
0.10 |
0.05 |
0.01 |
|
|
2.706 |
3.841 |
6.635 |
(参考数据与公式: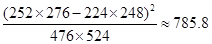
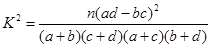 ;
;
|
|
女 |
男 |
合计 |
|
关心 |
|
|
500 |
|
不关心 |
|
|
500 |
|
合计 |
|
524 |
1000 |
(2)已知校团委有青年志愿者100名,他们已参加活动的情况记录如下:
|
参加活动次数 |
1 |
2 |
3 |
|
人数 |
10 |
50 |
40 |
(i)从志愿者中任选两名学生,求他们参加活动次数恰好相等的概率;
(ii)从志愿者中任选两名学生,用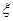 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量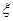 的分布列及数学期望
的分布列及数学期望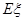 .
.
某中学号召本校学生在本学期参加市创办卫生城的相关活动,学校团委对该校学生是否关心创卫活动用简单抽样方法调查了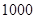 位学生(关心与不关心的各一半),
位学生(关心与不关心的各一半),
结果用二维等高条形图表示,如图.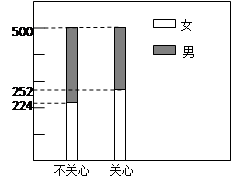
(1)完成列联表,并判断能否有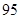 ℅的把握认为是否关心创卫活动与性别有关?
℅的把握认为是否关心创卫活动与性别有关?
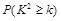 | 0.10 | 0.05 | 0.01 |
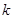 | 2.706 | 3.841 | 6.635 |
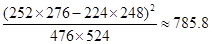
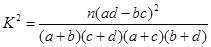 ;
;| | 女 | 男 | 合计 |
| 关心 | | | 500 |
| 不关心 | | | 500 |
| 合计 | | 524 | 1000 |
| 参加活动次数 | 1 | 2 | 3 |
| 人数 | 10 | 50 | 40 |
 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望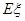 .
.A.
| B.
| C.
| D.
|
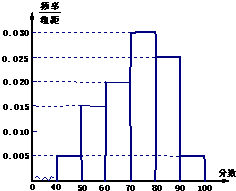 某校从高一年级期末考试的学生中抽出60名学生,其成绩(均为整数)的频率分布直方图如图所示:
某校从高一年级期末考试的学生中抽出60名学生,其成绩(均为整数)的频率分布直方图如图所示:一、选择题
1.A 2.C 3.A 4.C 5.D 6.C 7.B 8.C 9.A 10.A
11.D 12.D
二、填空题
13. 10
14.%20数学文科.files/image203.gif) 15. 4 16.
15. 4 16.%20数学文科.files/image205.gif)
三、解答题
17.解:(Ⅰ)%20数学文科.files/image133.gif) 的内角和
的内角和%20数学文科.files/image208.gif) ,由
,由%20数学文科.files/image210.gif) 得
得%20数学文科.files/image212.gif) .
.
应用正弦定理,知
%20数学文科.files/image214.gif) ,
,
%20数学文科.files/image216.gif) .
.
因为%20数学文科.files/image218.gif) ,
,
所以%20数学文科.files/image220.gif) ,
,
(Ⅱ)因为%20数学文科.files/image222.gif)
%20数学文科.files/image224.gif) ,
,
所以,当%20数学文科.files/image226.gif) ,即
,即%20数学文科.files/image228.gif) 时,
时,%20数学文科.files/image141.gif) 取得最大值
取得最大值%20数学文科.files/image231.gif) .
.
18.解:(Ⅰ)总体平均数为
%20数学文科.files/image233.gif) .
.
(Ⅱ)设%20数学文科.files/image235.gif) 表示事件“样本平均数与总体平均数之差的绝对值不超过
表示事件“样本平均数与总体平均数之差的绝对值不超过
从总体中抽取2个个体全部可能的基本结果有:%20数学文科.files/image237.gif) ,
,%20数学文科.files/image239.gif) ,
,%20数学文科.files/image241.gif) ,
,%20数学文科.files/image243.gif) ,
,%20数学文科.files/image245.gif) ,
,%20数学文科.files/image247.gif) ,
,%20数学文科.files/image249.gif) ,
,%20数学文科.files/image251.gif) ,
,%20数学文科.files/image253.gif) ,
,%20数学文科.files/image255.gif) ,
,%20数学文科.files/image257.gif) ,
,%20数学文科.files/image259.gif) ,
,%20数学文科.files/image261.gif) ,
,%20数学文科.files/image263.gif) ,
,%20数学文科.files/image265.gif) .共15个基本结果.
.共15个基本结果.
事件%20数学文科.files/image235.gif) 包括的基本结果有:
包括的基本结果有:%20数学文科.files/image243.gif) ,
,%20数学文科.files/image245.gif) ,
,%20数学文科.files/image249.gif) ,
,%20数学文科.files/image251.gif) ,
,%20数学文科.files/image253.gif) ,
,%20数学文科.files/image255.gif) ,
,%20数学文科.files/image257.gif) .共有7个基本结果.
.共有7个基本结果.
所以所求的概率为
%20数学文科.files/image268.gif) .
.
%20数学文科.files/image269.gif) 19.解:(Ⅰ) 由三视图可知,四棱锥
19.解:(Ⅰ) 由三视图可知,四棱锥%20数学文科.files/image146.gif) 的底面是边长为1的正方形,
的底面是边长为1的正方形,
侧棱%20数学文科.files/image271.gif) 底面
底面%20数学文科.files/image273.gif) ,且
,且%20数学文科.files/image275.gif) .
.
∴%20数学文科.files/image277.gif) ,
,
即四棱锥%20数学文科.files/image146.gif) 的体积为
的体积为%20数学文科.files/image279.gif) .
.
(Ⅱ) 连结%20数学文科.files/image281.gif) 、
、%20数学文科.files/image283.gif) ,
,%20数学文科.files/image285.gif)
∵%20数学文科.files/image273.gif) 是正方形,
是正方形,
∴%20数学文科.files/image287.gif) 是
是%20数学文科.files/image289.gif) 的中点,且
的中点,且%20数学文科.files/image148.gif) 是
是%20数学文科.files/image150.gif) 的中点
的中点
∴%20数学文科.files/image293.gif)
%20数学文科.files/image295.gif)
∴%20数学文科.files/image297.gif)
(Ⅲ)不论点%20数学文科.files/image148.gif) 在何位置,都有
在何位置,都有%20数学文科.files/image161.gif) .
.
证明如下:∵%20数学文科.files/image273.gif) 是正方形,∴
是正方形,∴%20数学文科.files/image300.gif) .
.
∵%20数学文科.files/image271.gif) 底面
底面%20数学文科.files/image273.gif) ,且
,且%20数学文科.files/image302.gif) 平面
平面%20数学文科.files/image273.gif) ,∴
,∴%20数学文科.files/image305.gif) .
.
又∵%20数学文科.files/image307.gif) ,∴
,∴%20数学文科.files/image309.gif) 平面
平面%20数学文科.files/image311.gif) .
.
∵不论点%20数学文科.files/image148.gif) 在何位置,都有
在何位置,都有%20数学文科.files/image314.gif)
%20数学文科.files/image316.gif) 平面
平面%20数学文科.files/image311.gif) .
.
∴不论点%20数学文科.files/image148.gif) 在何位置,都有
在何位置,都有%20数学文科.files/image161.gif) .
.
20.解:(Ⅰ)%20数学文科.files/image318.gif)
%20数学文科.files/image169.gif) ,
,%20数学文科.files/image321.gif)
%20数学文科.files/image323.gif) ,
,
%20数学文科.files/image321.gif)
%20数学文科.files/image325.gif) ,又
,又%20数学文科.files/image167.gif) ,
,%20数学文科.files/image321.gif)
%20数学文科.files/image328.gif) ,
,
%20数学文科.files/image321.gif) 数列
数列%20数学文科.files/image173.gif) 是以为
是以为%20数学文科.files/image330.gif) 首项,
首项,%20数学文科.files/image330.gif) 为公比的等比数列.
为公比的等比数列.
(Ⅱ)由(Ⅰ)知%20数学文科.files/image332.gif) ,即
,即%20数学文科.files/image334.gif) ,
,%20数学文科.files/image321.gif)
%20数学文科.files/image337.gif) .
.
设%20数学文科.files/image339.gif) …
…%20数学文科.files/image341.gif) , ①
, ①
则%20数学文科.files/image343.gif) …
…%20数学文科.files/image345.gif) ,②
,②
由①%20数学文科.files/image347.gif) ②得
②得
%20数学文科.files/image349.gif) …
…%20数学文科.files/image351.gif) ,
,
%20数学文科.files/image321.gif)
%20数学文科.files/image354.gif) .又
.又%20数学文科.files/image356.gif) …
…%20数学文科.files/image358.gif) .
.
%20数学文科.files/image321.gif) 数列
数列%20数学文科.files/image175.gif) 的前
的前%20数学文科.files/image111.gif) 项和
项和 %20数学文科.files/image361.gif) .
.
21.解:(Ⅰ)%20数学文科.files/image363.gif) .
.
因为%20数学文科.files/image365.gif) 是函数
是函数%20数学文科.files/image143.gif) 的极值点,所以
的极值点,所以%20数学文科.files/image368.gif) ,即
,即%20数学文科.files/image370.gif) ,因此
,因此%20数学文科.files/image372.gif) .
.
经验证,当%20数学文科.files/image372.gif) 时,
时,%20数学文科.files/image365.gif) 是函数
是函数%20数学文科.files/image143.gif) 的极值点.
的极值点.
(Ⅱ)由题设,%20数学文科.files/image377.gif) .
.
当%20数学文科.files/image379.gif) 在区间
在区间%20数学文科.files/image381.gif) 上的最大值为
上的最大值为%20数学文科.files/image383.gif) 时,
时,
%20数学文科.files/image385.gif) ,
,
即%20数学文科.files/image387.gif) .
.
故得%20数学文科.files/image389.gif) .
.
反之,当%20数学文科.files/image389.gif) 时,对任意
时,对任意%20数学文科.files/image392.gif) ,
,
%20数学文科.files/image394.gif)
%20数学文科.files/image396.gif)
%20数学文科.files/image398.gif)
%20数学文科.files/image400.gif) ,
,
而%20数学文科.files/image402.gif) ,故
,故%20数学文科.files/image379.gif) 在区间
在区间%20数学文科.files/image381.gif) 上的最大值为
上的最大值为%20数学文科.files/image383.gif) .
.
综上,%20数学文科.files/image188.gif) 的取值范围为
的取值范围为%20数学文科.files/image408.gif) .
.
22.解:(Ⅰ)设椭圆的半焦距为%20数学文科.files/image410.gif) ,依题意
,依题意%20数学文科.files/image412.gif)
%20数学文科.files/image414.gif) ,
,%20数学文科.files/image321.gif) 所求椭圆方程为
所求椭圆方程为%20数学文科.files/image417.gif) .
.
(Ⅱ)设%20数学文科.files/image419.gif) ,
,%20数学文科.files/image421.gif) .
.
(1)当%20数学文科.files/image423.gif) 轴时,
轴时,%20数学文科.files/image425.gif) .
.
(2)当%20数学文科.files/image427.gif) 与
与%20数学文科.files/image429.gif) 轴不垂直时,
轴不垂直时,
设直线%20数学文科.files/image427.gif) 的方程为
的方程为%20数学文科.files/image432.gif) .
.
由已知%20数学文科.files/image434.gif) ,得
,得%20数学文科.files/image436.gif) .
.
把%20数学文科.files/image432.gif) 代入椭圆方程,整理得
代入椭圆方程,整理得%20数学文科.files/image439.gif) ,
,
%20数学文科.files/image441.gif) ,
,%20数学文科.files/image443.gif) .
.
%20数学文科.files/image445.gif)
%20数学文科.files/image447.gif)
%20数学文科.files/image449.gif)
%20数学文科.files/image451.gif) .
.
当且仅当%20数学文科.files/image453.gif) ,即
,即%20数学文科.files/image455.gif) 时等号成立.当
时等号成立.当%20数学文科.files/image457.gif) 时,
时,%20数学文科.files/image425.gif) ,
,
综上所述%20数学文科.files/image460.gif) .
.
%20数学文科.files/image321.gif) 当
当%20数学文科.files/image463.gif) 最大时,
最大时,%20数学文科.files/image465.gif) 面积取最大值
面积取最大值%20数学文科.files/image467.gif) .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com