(2012•成都一模)已知函数f(x)在[a,b]上连续,定义
| | f1(x)=f(t)min,x∈[a,b],a≤t≤x | | f2(x)=f(t)max,x∈[a,b],a≤t≤x |
| |
;其中f(x)
min(x∈D)表示f(x)在D上的最小值,f(x)
max(x∈D)表示f(x)在D上的最大值.若存在最小正整数k使得f
2(x)-f
1(x)≤k(x-a)对任意的x∈[a,b]成立,则称函数f(x)为[a,b]上的“k阶收缩函数”.有下列命题:
①若f(x)=cosx,x∈[0,π],则f
1(x)=1,x∈[0,π];
②若f(x)=2
x,x∈[-1,4],则
f2(x)=2x,x∈[-1,4]③f(x)=x为[1,2]上的1阶收缩函数;
④f(x)=x
2为[1,4]上的5阶收缩函数.
其中你认为正确的所有命题的序号为
②③④
②③④
.

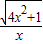 (x>0).
(x>0).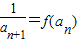 ,求an;
,求an;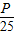 成立.
成立.