
题目列表(包括答案和解析)
 .
.已知函数![]() ,x
,x![]() 其中a>0.
其中a>0.
(I)求函数![]() 的单调区间;
的单调区间;
(II)若函数![]() 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围;
(III)当a=1时,设函数![]() 在区间
在区间![]() 上的最大值为M(t),最小值为m(t),记g(t)=M(t)-m(t),求函数g(t)在区间
上的最大值为M(t),最小值为m(t),记g(t)=M(t)-m(t),求函数g(t)在区间![]() 上的最小值。
上的最小值。
已知函数 其中a>0.
其中a>0.
(I)求函数f(x)的单调区间;
(II)若函数f(x)在区间(-2,0)内恰有两个零点,求a的取值范围;
(III)当a=1时,设函数f(x)在区间[t,t+3]上的最大值为M(t),最小值为m(t),记g(t)=M(t)-m(t),求函数g(t)在区间[-3,-1]上的最小值。
【考点定位】本小题主要考查导数的运算,利用导数研究函数的单调性、函数的零点,函数的最值等基础知识.考查函数思想、分类讨论思想.考查综合分析和解决问题的能力.
 x3+
x3+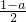 x2-ax-a,其中a>0.
x2-ax-a,其中a>0.| 1 |
| 3 |
| 1-a |
| 2 |
一、选择题:
1―5 ACBBD 6―10 BCDAC
二、填空题:
11.60 12.试题.files/image132.gif) 13.―
13.―试题.files/image060.gif) 14.
14.试题.files/image135.gif)
15.2 16.试题.files/image137.gif) 17.
17.试题.files/image139.gif)
三、解答题:
18.解:(I)试题.files/image141.gif)
|