
题目列表(包括答案和解析)
已知函数![]() =
=![]() ,
,![]() .
.
(Ⅰ)求函数![]() 在区间
在区间![]() 上的值域;
上的值域;
(Ⅱ)是否存在实数![]() ,对任意给定的
,对任意给定的![]() ,在区间
,在区间![]() 上都存在两个不同的
上都存在两个不同的![]() ,使得
,使得![]() 成立.若存在,求出
成立.若存在,求出![]() 的取值范围;若不存在,请说明理由;
的取值范围;若不存在,请说明理由;
(Ⅲ)给出如下定义:对于函数![]() 图象上任意不同的两点
图象上任意不同的两点![]() ,如果对于函数
,如果对于函数![]() 图象上的点
图象上的点![]() (其中
(其中![]() 总能使得
总能使得![]() 成立,则称函数具备性质“
成立,则称函数具备性质“![]() ”,试判断函数
”,试判断函数![]() 是不是具备性质“
是不是具备性质“![]() ”,并说明理由.
”,并说明理由.
(1)已知:![]() ,求函数f(x)的单调区间和值域;
,求函数f(x)的单调区间和值域;
(2)a≥1,函数g(x)=x3-3a2x-2a,x∈[0,1],判断函数g(x)的单调性并予以证明;
(3)当a≥1时,上述(1)、(2)小题中的函数f(x)、g(x),若对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求a的取值范围.
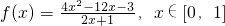 ,求函数f(x)的单调区间和值域;
,求函数f(x)的单调区间和值域; ,求函数f(x)的单调区间和值域;
,求函数f(x)的单调区间和值域; ,求函数f(x)的单调区间和值域;
,求函数f(x)的单调区间和值域;一、选择题:
CCBCD CCBCA DD
二、填空题:
13、.files/image261.gif) 14、
14、.files/image263.gif) 15、-6 16、
15、-6 16、.files/image265.gif)
三、解答题:
17.解:(Ⅰ)
∵.files/image267.gif) 2分
2分
=1+.files/image269.gif) 4分
4分
∴最小正周期是.files/image271.gif) ,最小值为
,最小值为.files/image273.gif) .
6分
.
6分
(Ⅱ)解法一:因为.files/image275.gif) ,
,
令.files/image277.gif) 8分
8分
得函数在.files/image193.gif) 上的单调增区间为
上的单调增区间为.files/image279.gif) 。
12分
。
12分
解法二:作函数.files/image275.gif) 图象,由图象得函数
图象,由图象得函数.files/image120.gif) 在区间
在区间.files/image193.gif) 上的上的单调
上的上的单调
.files/image282.jpg)
.files/image284.gif) 10分
10分
如果.files/image200.gif) 为真,
为真,.files/image202.gif) 为假,则C的取值范围为
为假,则C的取值范围为.files/image286.gif) 。 12分
。 12分
19、解:本小题主要考查正弦定理、余弦定理等基础知识,同时考查利用三角公式进行恒等变形的技能和运算能力.
设E为BC的中点,连接DE,则DE//AB,且DE=.files/image288.gif) 2分
2分
在△BDE中利用余弦定理可得:
BD2=BE2+ED2-2BE?ED?cos∠BED,
.files/image290.gif)
.files/image292.gif) 6分
6分
.files/image294.gif) 12分
12分
20、解:(Ⅰ)由已知得.files/image296.gif) ,
,.files/image298.gif) ,……………………1分
,……………………1分
故.files/image300.gif) .……………………………………4分
.……………………………………4分
(Ⅱ)由(Ⅰ)得,.files/image302.gif) ,……………………………………………5分
,……………………………………………5分
再由已知得,等比数列.files/image304.gif) 的公比
的公比.files/image306.gif) ,
,.files/image308.gif) ………6分
………6分
.files/image310.gif)
.files/image312.gif) ……………………………………8分
……………………………………8分
(III)由(Ⅰ)得.files/image314.gif) .………………………………9分
.………………………………9分
假设数列中存在相邻三项.files/image316.gif) 成等比数列,
成等比数列,
则.files/image318.gif) ,即
,即.files/image320.gif) .…………10分
.…………10分
推出.files/image322.gif) 矛盾.所以数列
矛盾.所以数列.files/image324.gif) 中任意不同的三项都不可能成等比数列.12分
中任意不同的三项都不可能成等比数列.12分
21、解:对函数.files/image241.gif) 求导,得
求导,得.files/image326.gif)
.files/image328.gif)
令.files/image330.gif) 解得
解得 .files/image332.gif) 或
或.files/image334.gif) 2分
2分
当.files/image178.gif) 变化时,
变化时,.files/image337.gif) 、
、.files/image241.gif) 的变化情况如下表:
的变化情况如下表:
x
0
.files/image340.gif)
.files/image342.gif)
.files/image344.gif)
.files/image346.gif)
.files/image337.gif)
.files/image348.gif)
0
.files/image350.gif)
.files/image241.gif)
.files/image352.gif)
ㄋ
.files/image354.gif)
ㄊ
.files/image356.gif)
4分
所以,当.files/image358.gif) 时,
时,.files/image241.gif) 是减函数;当
是减函数;当.files/image361.gif) 时,
时,.files/image241.gif) 是增函数;
是增函数;
当.files/image363.gif) 时,
时,.files/image241.gif) 的值域为
的值域为.files/image365.gif) 。
6分
。
6分
(Ⅱ)对函数.files/image367.gif) 求导,得
求导,得 .files/image369.gif)
因此.files/image243.gif) ,当
,当.files/image363.gif) 时,
时, .files/image373.gif)
因此当.files/image363.gif) 时,
时,.files/image367.gif) 为减函数,
7分
为减函数,
7分
.files/image376.jpg)
解.files/image378.gif) 式得
式得 .files/image243.gif) 或
或.files/image381.gif) 解
解.files/image383.gif) 式得
式得 .files/image385.gif) 又
又.files/image243.gif) ,
,
故:.files/image184.gif) 的取值范围为
的取值范围为.files/image388.gif) 。
12分
。
12分
22、(本小题满分14分).
解: (Ⅰ)函数.files/image120.gif) 的定义域是
的定义域是.files/image391.gif) ,
, .files/image393.gif) …………2分
…………2分
当.files/image395.gif) 时,∵
时,∵.files/image397.gif) ∴
∴.files/image399.gif) 即
即 .files/image401.gif)
这说明函数.files/image120.gif) 在区间
在区间.files/image403.gif) 上是减函数 ……………4分
上是减函数 ……………4分
当.files/image405.gif) 时,
时,.files/image407.gif) …………5分
…………5分
当.files/image409.gif) 时,
∵
时,
∵.files/image411.gif) ∴
∴.files/image399.gif) 即
即 .files/image413.gif)
这说明函数.files/image120.gif) 在区间
在区间.files/image415.gif) 上是增函数 ………………6分
上是增函数 ………………6分
故当.files/image405.gif) 时,
时,.files/image120.gif) 取得最小值
取得最小值.files/image346.gif) ……7分
……7分
(Ⅱ)由(1)知,当.files/image419.gif) 时,
时,.files/image421.gif) ……8分
……8分
而 .files/image423.gif) ,
,.files/image425.gif) ,因此
,因此.files/image427.gif)
∴.files/image429.gif) ①
…12分
①
…12分
又.files/image431.gif)
.files/image433.gif)
.files/image435.gif)
.files/image437.gif)
∴.files/image439.gif) ②
…13分
②
…13分
综合①、②得 .files/image441.gif) 成立
…14分
成立
…14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com