如图所示，质量为M的平板车P高h，质量为m的小物块Q的大小不计，位于平板车的左端，系统原来静止在光滑水平面地面上．一不可伸长的轻质细绳长为R，一端悬于Q正上方高为R处，另一端系一质量也为m的小球（大小不计）．今将小球拉至悬线与竖直位置成60°角，由静止释放，小球到达最低点时与Q的碰撞时间极短，且无机械能损失，已知Q离开平板车时速度大小是平板车速度的两倍，Q与P之间的动摩擦因数为μ，已知平板车的质量M：m=4：1，重力加速度为g．求：
（1）小物块Q离开平板车时，二者速度各为多大？
（2）平板车P的长度为多少？
（3）小物块Q落地时与小车的水平距离为多少？

查看答案和解析>>

如图所示，质量为M的平板车P高h，质量为m的小物块Q的大小不计，位于平板车的左端，系统原来静止在光滑水平面地面上．一不可伸长的轻质细绳长为R，一端悬于Q正上方高为R处，另一端系一质量也为m的小球（大小不计）．今将小球拉至悬线与竖直位置成60°角，由静止释放，小球到达最低点时与Q的碰撞时间极短，且无能量损失，已知Q离开平板车时速度大小是平板车速度的两倍，Q与P之间的动摩擦因数为μ，M：m=4：1，重力加速度为g．求：
（1）小物块Q离开平板车时速度为多大？
（2）平板车P的长度为多少？
（3）小物块Q落地时距小球的水平距离为多少？

查看答案和解析>>

（2005?诸城市模拟）如图所示，一辆长L=2m、高h=0.8m、质量为M=12kg的平顶车，车顶光滑，在牵引力为零时，仍在向前运动，车与路面间的动摩擦因数μ=0.3．当车速为v₀=7m/s时，把一个质量为m=1kg的物块（视为质点）轻轻放在车顶的前端．问物块落地时，落地点距车前端多远？（取g=10m/s²．）

查看答案和解析>>

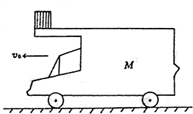如图所示，一辆长L=2m，高 h=0.8m，质量为 M=12kg 的平顶车，车顶面光滑，在牵引力为零时，仍在向前运动，设车运动时受到的阻力与它对地面的压力成正比，且比例系数μ=0.3．当车速为 v₀=7m/s 时，把一个质量为 m=1kg 的物块（视为质点）轻轻放在车顶的前端，并开始计时．那么，经过t=

 

s物块离开平顶车；物块落地时，落地点距车前端的距离为s=

 

m．

查看答案和解析>>

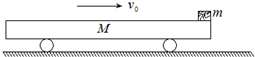如图所示，一辆长L=2m、高h=0.8m、质量为M=12kg的平顶车，车顶面光滑，车与水平长直路面间的动摩擦因数μ=0.3，车在路面上无动力的滑行，当车速为v₀=7m/s时，把一个质量为m=1kg的物块（视为质点）轻轻放在车顶的前端．从物块放上车开始计时，求
（1）物块经过多长时间着地？
（2）经过3s时间，物块离车前端多远？（物块着地后不再反弹，取g=10m/s²，计算结果保留2位有效数字）

查看答案和解析>>

14． A    15． A   16．C    17．A D   18．B D    19．A D   20．D    21．B

22． Ⅰ．单分子 ，36～40

Ⅱ.①29.9kΩ，(3分)②(a )外接，分压 (3分) (b )见下图，(3分)③变小(3分)

23．解：水从h高处落下可认为是自由落体运动，速度为v，则 （2分）

m/s    ①                                              （2分）

设在很短时间t内有质量为m的水落到石头上，以它为研究对象，设石头对水的平均作用力为F，取竖直向下为正方向，由动量定理得，②，而③        （6分）

由①②③式代入数据解得，N（2分）

根据牛顿第三定律可知，水对石头的反作用力=N． （2分）

24． 解：（1）小球由静止到最低点时，有（2分）（1分）

小球与物块Q相撞时: ，（1分）     ，（1分）

解得，，（2分）

Q在平板车上滑行的过程中，有（1分）  （1分）

小物块Q离开平板车时，速度为（1分）

（2）由能的转化和守恒定律，知（1分）

（1分）      解得，（1分）

（3）小物块Q在平板车上滑行过程中，对地位移为s，则:

（1分）     解得，（1分）

平抛时间（1分）   水平距离（1分）

Q落地点距小球的水平距离为（1分）

25．解:（1）在0―t₀带电粒子做匀速圆周运动其周期为   （2分）

则在t₀时间内转过的圆心角   位置坐标： （4分）

      （2）t₀―2t₀时间内带电粒子做匀速直线运动，2t₀―3t₀时间内带电粒子做匀速圆周运动，

转过的圆心角仍为；……．所以粒子从出发到再次回到原点所用的时间为t=8t₀．（3分）

由于带电粒子的速率不会改变，所以带电粒子从出发到再次回到原点的运动轨迹的

    长度s=8 v₀t₀．（3分）                                                   

     （3）由带电粒子的比荷可知粒子运动的周期  （2分）

 则在t₀时间内转过的圆心角   t₀时刻粒子第一次到达x轴速度方向沿y轴负方向，则在t₀―2t₀时间内沿y轴负方向做匀加速直线运动；在2t₀―3t₀时间内带电粒子又做匀速圆周运动，转过的圆心角仍为，由于速度增大，因此，此时运动的轨道半径大于第一次时的半径．在3t₀―4t₀时间内，带电粒子沿y轴正方向做匀减速直线运动，第二次到达x轴由对称性可知，在4t₀时速度又变为v₀；在4t₀―5t₀时间内又做圆周运动，第三次到达x轴时在坐标原点，设带电粒子在x轴上方做圆周运动的轨道半径为r₁，在x轴下方做圆周运动的轨道半径为r₂，由几何关系可知，要使带电粒子回到原点，则必须满足：

       （2分）                   解得：    （2分）

    又由于   （2分）    解得：   （2分）