
题目列表(包括答案和解析)
如图 是单位圆
是单位圆 上的点,
上的点, 分别是圆
分别是圆 与
与 轴的两交点,
轴的两交点, 为正三角形.
为正三角形.

(1)若 点坐标为
点坐标为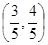 ,求
,求 的值;
的值;
(2)若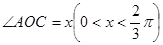 ,四边形
,四边形 的周长为
的周长为 ,试将
,试将 表示成
表示成 的函数,并求出
的函数,并求出 的最大值.
的最大值.
【解析】第一问利用设
∵ A点坐标为 ∴
∴  ,
,
(2)中 由条件知 AB=1,CD=2 ,
在 中,由余弦定理得
中,由余弦定理得 
∴ 
∵  ∴
∴  ,
,
∴ 当 时,即
当
时,即
当 时 , y有最大值5. .
时 , y有最大值5. .
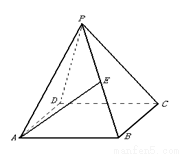
如图,在正四棱锥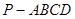 中,
中,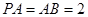 .
.
(1)求该正四棱锥的体积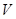 ;
;
(2)设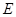 为侧棱
为侧棱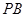 的中点,求异面直线
的中点,求异面直线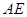 与
与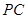
所成角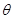 的大小.
的大小.
【解析】第一问利用设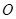 为底面正方形
为底面正方形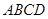 中心,则
中心,则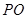 为该正四棱锥的高由已知,可求得
为该正四棱锥的高由已知,可求得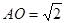 ,
,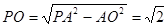
所以,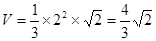
第二问设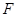 为
为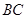 中点,连结
中点,连结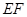 、
、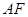 ,
,
可求得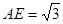 ,
,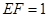 ,
,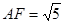 ,
,
在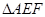 中,由余弦定理,得
中,由余弦定理,得
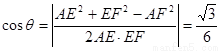 .
.
所以,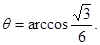
如图,测量河对岸的塔高 时,可以选与塔底
时,可以选与塔底 在同一水平面内的两个测点
在同一水平面内的两个测点 .现测得
.现测得
 ,并在点
,并在点 测得塔顶
测得塔顶 的仰角为
的仰角为 ,
求塔高
,
求塔高 (精确到
(精确到 ,
, )
)

【解析】本试题主要考查了解三角形的运用,利用正弦定理在 中,得到
中,得到 ,然后在
,然后在 中,利用正切值可知
中,利用正切值可知
解:在 中,
中,
由正弦定理得: ,所以
,所以 
在 中,
中,
如图,点P为斜三棱柱ABC-A1B1C1的侧棱BB1上一点,PM⊥BB1交AA1于点M,PN⊥BB1交CC1于点N.
(1)求证:CC1⊥MN.
 (2)在任意△DEF中,
(2)在任意△DEF中,![]() 有由余弦定理DE2=DF2+EF2-2DF·EFcos∠DFE,拓展到空间,类比三角形的余弦定理,写出一个斜三棱柱的三个侧面积与其中两个侧面所成的二面角之间的关系式,并加以证明.
有由余弦定理DE2=DF2+EF2-2DF·EFcos∠DFE,拓展到空间,类比三角形的余弦定理,写出一个斜三棱柱的三个侧面积与其中两个侧面所成的二面角之间的关系式,并加以证明.
在△ABC中,角A、B、C的对边分别为a、b、c,向量 =(sinA,b+c),
=(sinA,b+c), =(a-c,sinC-sinB),满足
=(a-c,sinC-sinB),满足 =
=
(Ⅰ)求角B的大小;
(Ⅱ)设 =(sin(C+
=(sin(C+ ),
), ),
),  =(2k,cos2A) (k>1),
=(2k,cos2A) (k>1),  有最大值为3,求k的值.
有最大值为3,求k的值.
【解析】本试题主要考查了向量的数量积和三角函数,以及解三角形的综合运用
第一问中由条件|p +q |=| p -q |,两边平方得p·q=0,又
p=(sinA,b+c),q=(a-c,sinC-sinB),代入得(a-c)sinA+(b+c)(sinC-sinB)=0,
根据正弦定理,可化为a(a-c)+(b+c)(c-b)=0,
即 ,又由余弦定理
,又由余弦定理 =2acosB,所以cosB=
=2acosB,所以cosB= ,B=
,B=
第二问中,m=(sin(C+ ),
), ),n=(2k,cos2A) (k>1),m·n=2ksin(C+
),n=(2k,cos2A) (k>1),m·n=2ksin(C+ )+
)+ cos2A=2ksin(C+B) +
cos2A=2ksin(C+B) + cos2A
cos2A
=2ksinA+ -
- =-
=- +2ksinA+
+2ksinA+ =-
=- +
+ (k>1).
(k>1).
而0<A< ,sinA∈(0,1],故当sin=1时,m·n取最大值为2k-
,sinA∈(0,1],故当sin=1时,m·n取最大值为2k- =3,得k=
=3,得k= .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com