题目列表(包括答案和解析)
（07年陕西卷理）(12分)
已知各项全不为零的数列{ak}的前k项和为Sk,且Sk＝
N*),其中a1=1.
(Ⅰ)求数列{ak}的通项公式;
(Ⅱ)对任意给定的正整数n(n≥2),数列{bk}满足
（k=1,2,…，n-1）,b1=1.
求b1+b2+…+bn.
(本小题满分12分)
已知各项全不为零的数列{ak}的前k项和为Sk,且Sk＝
N*),其中a1=1.
(Ⅰ)求数列{ak}的通项公式;
(Ⅱ)对任意给定的正整数n(n≥2),数列{bk}满足
（k=1,2,…，n-1）,b1=1.
求b1+b2+…+bn.
（07年陕西卷理）(12分)
已知各项全不为零的数列{ak}的前k项和为Sk,且Sk＝
N*),其中a1=1.
(Ⅰ)求数列{ak}的通项公式;
(Ⅱ)对任意给定的正整数n(n≥2),数列{bk}满足
（k=1,2,…，n-1）,b1=1.
求b1+b2+…+bn.
已知等差数列{an}的前5项和为105,且a10=2a5.
(1)求数列{an}的通项公式;
(2)对任意m∈N*,将数列{an}中不大于72m的项的个数记为bm,求数列{bm}的前m项和Sm.
已知数列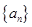
满足
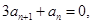
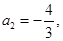则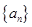的前10项和等于（ ）
A．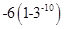
B．
C．
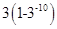D．
必修
一、填空题
1、8 2、
3、2|P| 4、
5、向左移
，在把各点的横坐标伸长到原来的3倍
6、18 7、120度 8、
9、
10、②④ 11、
12、
13、
14、
二、解答题
15．解：（Ⅰ）
＝
．………… 4分
由
，得
．
∴函数
的单调增区间为 
．………… 7分
（Ⅱ）由
，得
．
∴
．
………………………………………… 10分
∴
，或
，
即
或
．
∵
，∴
． …………………………………………… 14分
16．解：（Ⅰ）n≥2时，
． ………………… 4分
n＝1时，
，适合上式，
∴
．
………………… 5分
（Ⅱ）
，
．
………………… 8分
即
．
∴数列
是首项为4、公比为2的等比数列． ………………… 10分
，∴
．……………… 12分
Tn＝
＝
．
………………… 14分
17、⑴ ⑵ ⑶不能
18、⑴
⑵
=1时，
的最大值为20200，=10时，的最小值为12100。
19、⑴易知AB恒过椭圆的右焦点F（
，0） ⑵ S= 
⑶存在
。
20、⑴
⑵
或
⑶（
，
）
附加题选修参考答案
1、⑴BB
=
， ⑵ 
2、⑴
⑵ 
，
，
，EX=1
3、 
4、⑴ ⑵ MN=2
5、⑴特征值为2和3 ，对应的特征向量分别为
及
，
⑵ 
，椭圆在矩阵的作用下对应得新方程为
6、提示：
，然后用基本不等式或柯西不等式即可。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com