
题目列表(包括答案和解析)
| 2 |
14
| ||
| 3 |
| cosA |
| cosB |
| b |
| a |
| 4 |
| 3 |
| 7 |
| 2 |
| b |
| c |
| c |
| b |
| 5 |
| 2 |
14
| ||
| 3 |
| cosA |
| cosB |
| b |
| a |
| 4 |
| 3 |
| 7 |
| 2 |
| b |
| c |
| c |
| b |
| 5 |
 ;②在△ABC中,若b=8,c=5,A=60°,则△ABC的外接圆半径等于
;②在△ABC中,若b=8,c=5,A=60°,则△ABC的外接圆半径等于 ;③在△ABC中,若c=5,
;③在△ABC中,若c=5,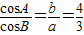 ,则△ABC的内切圆的半径为2;④在△ABC中,若AB=4,AC=7,BC=9,则BC边的中线
,则△ABC的内切圆的半径为2;④在△ABC中,若AB=4,AC=7,BC=9,则BC边的中线 ;⑤设三角形ABC的BC边上的高AD=BC,a、b、c分别表示角A、B、C对应的三边,则
;⑤设三角形ABC的BC边上的高AD=BC,a、b、c分别表示角A、B、C对应的三边,则 的取值范围是
的取值范围是 .其中正确说法的序号是 (注:把你认为是正确的序号都填上).
.其中正确说法的序号是 (注:把你认为是正确的序号都填上).| 1 | 2 |
 r(a+b+c),根据类比思想,若四面体的内切球半径为R,四个面的面积分别为S1,S2,S3,S4,则此四面体的体积V=________.
r(a+b+c),根据类比思想,若四面体的内切球半径为R,四个面的面积分别为S1,S2,S3,S4,则此四面体的体积V=________.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com