
题目列表(包括答案和解析)
已知函数f(x)=4x3+3tx2-6t2x+t-1,x∈R,其中t∈R.
(1)当t=1时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(2)当t≠0时,求f(x)的单调区间;
(3)证明:对任意t∈(0,+∞),f(x)在区间(0,1)内均存在零点.
如右图 ,A、B、C、D为空间四点.在△ABC中,AB=2,AC=BC=.等边三角形ADB以AB为轴运动.
,A、B、C、D为空间四点.在△ABC中,AB=2,AC=BC=.等边三角形ADB以AB为轴运动.
(1)当平面ADB⊥平面ABC时,求CD;
(2)当△ADB转动时,是否总有AB⊥CD?
证明你的结论.
21.(本小题满分14分)
定义数列{an}如下:a1=2,an+1=an2-an+1,n∈N*.证明:
(1)对于n∈N* 恒有an+1>an 成立;
(2)当n∈N*时,有an+1=anan-1…a2a1+1成立;
(3)
(本小题满分12分)
已知函数f(x)=cox2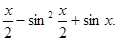
(Ⅰ)求函数f(x)的最小正周期;
(2)当x0∈(0,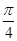 )且f(x0)=
)且f(x0)=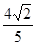 时,求f(x0+
时,求f(x0+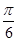 )的值.
)的值.
设U=R,A={ },B={
},B={ },求
},求
(1)?UB;(2)当B?A时,求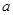 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com