
题目列表(包括答案和解析)
已知中心在坐标原点,焦点在 轴上的椭圆C;其长轴长等于4,离心率为
轴上的椭圆C;其长轴长等于4,离心率为 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点 (0,1), 问是否存在直线
(0,1), 问是否存在直线 与椭圆
与椭圆 交于
交于 两点,且
两点,且 ?若存在,求出
?若存在,求出 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
【解析】本试题主要考查了椭圆的方程的求解,直线与椭圆的位置关系的运用。
第一问中,可设椭圆的标准方程为
则由长轴长等于4,即2a=4,所以a=2.又 ,所以
,所以 ,
,
又由于
所求椭圆C的标准方程为
第二问中,
假设存在这样的直线 ,设
,设 ,MN的中点为
,MN的中点为
因为|ME|=|NE|所以MN EF所以
EF所以
(i)其中若 时,则K=0,显然直线
时,则K=0,显然直线 符合题意;
符合题意;
(ii)下面仅考虑 情形:
情形:
由 ,得,
,得,
 ,得
,得
代入1,2式中得到范围。
(Ⅰ) 可设椭圆的标准方程为
则由长轴长等于4,即2a=4,所以a=2.又 ,所以
,所以 ,
,
又由于
所求椭圆C的标准方程为
(Ⅱ) 假设存在这样的直线 ,设
,设 ,MN的中点为
,MN的中点为
因为|ME|=|NE|所以MN EF所以
EF所以
(i)其中若 时,则K=0,显然直线
时,则K=0,显然直线 符合题意;
符合题意;
(ii)下面仅考虑 情形:
情形:
由 ,得,
,得,
 ,得
,得 ……② ……………………9分
……② ……………………9分
则 .
.
代入①式得,解得 ………………………………………12分
………………………………………12分
代入②式得 ,得
,得 .
.
综上(i)(ii)可知,存在这样的直线 ,其斜率k的取值范围是
,其斜率k的取值范围是
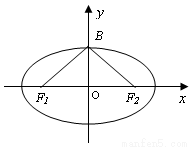
如图,已知椭圆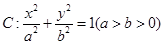 的焦点和上顶点分别为
的焦点和上顶点分别为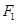 、
、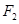 、
、 ,我们称
,我们称 为椭圆
为椭圆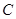 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
(1)已知椭圆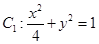 和
和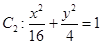 ,判断
,判断 与
与 是否相似,如果相似则求出
是否相似,如果相似则求出 与
与 的相似比,若不相似请说明理由;
的相似比,若不相似请说明理由;
(2)若与椭圆 相似且半短轴长为
相似且半短轴长为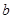 的椭圆为
的椭圆为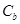 ,且直线
,且直线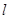 与椭圆为
与椭圆为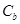 相交于两点
相交于两点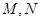 (异于端点),试问:当
(异于端点),试问:当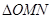 面积最大时,
面积最大时,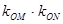 是否与
是否与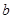 有关?并证明你的结论.
有关?并证明你的结论.
(3)根据与椭圆 相似且半短轴长为
相似且半短轴长为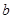 的椭圆
的椭圆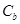 的方程,提出你认为有价值的相似椭圆之间的三种性质(不需证明);
的方程,提出你认为有价值的相似椭圆之间的三种性质(不需证明);
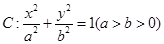 的焦点和上顶点分别为
的焦点和上顶点分别为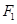 、
、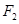 、
、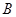 ,我们称
,我们称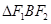 为椭圆
为椭圆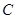 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比. 和
和 ,判断
,判断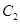 与
与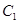 是否相似,如果相似则求出
是否相似,如果相似则求出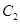 与
与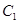 的相似比,若不相似请说明理由;
的相似比,若不相似请说明理由;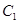 相似且半短轴长为
相似且半短轴长为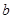 的椭圆为
的椭圆为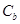 ,且直线
,且直线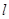 与椭圆为
与椭圆为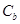 相交于两点
相交于两点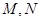 (异于端点),试问:当
(异于端点),试问:当 面积最大时,
面积最大时,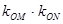 是否与
是否与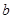 有关?并证明你的结论.
有关?并证明你的结论.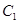 相似且半短轴长为
相似且半短轴长为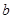 的椭圆
的椭圆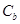 的方程,提出你认为有价值的相似椭圆之间的三种性质(不需证明);
的方程,提出你认为有价值的相似椭圆之间的三种性质(不需证明);
已知函数 =
= .
.
(Ⅰ)当 时,求不等式
时,求不等式
 ≥3的解集;
≥3的解集;
(Ⅱ) 若 ≤
≤ 的解集包含
的解集包含 ,求
,求 的取值范围.
的取值范围.
【命题意图】本题主要考查含绝对值不等式的解法,是简单题.
【解析】(Ⅰ)当 时,
时, =
= ,
,
当 ≤2时,由
≤2时,由 ≥3得
≥3得 ,解得
,解得 ≤1;
≤1;
当2< <3时,
<3时, ≥3,无解;
≥3,无解;
当 ≥3时,由
≥3时,由 ≥3得
≥3得 ≥3,解得
≥3,解得 ≥8,
≥8,
∴ ≥3的解集为{
≥3的解集为{ |
| ≤1或
≤1或 ≥8};
≥8};
(Ⅱ)  ≤
≤
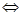
 ,
,
当 ∈[1,2]时,
∈[1,2]时, =
= =2,
=2,
∴ ,有条件得
,有条件得 且
且 ,即
,即 ,
,
故满足条件的 的取值范围为[-3,0]
的取值范围为[-3,0]
设向量 ,
, ,其中
,其中 ,由不等式
,由不等式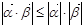 恒成立,可以证明(柯西)不等式
恒成立,可以证明(柯西)不等式 (当且仅当
(当且仅当 ∥
∥ ,即
,即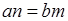 时等号成立),己知
时等号成立),己知 ,若
,若 恒成立,利用可西不等式可求得实数
恒成立,利用可西不等式可求得实数 的取值范围是
的取值范围是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com