轴.y轴在竖直方向.在水平面上方存在与x轴平行的匀强电场.一个质量m = 2.0×10-3kg.电量q = 2.0×10-6C的带正电的物体.从O点开始以一定的初速度沿着x轴正方向做直线运动.其位移随——青夏教育精英家教网—

轴.y轴在竖直方向.在水平面上方存在与x轴平行的匀强电场.一个质量m = 2.0×10-3kg.电量q = 2.0×10-6C的带正电的物体.从O点开始以一定的初速度沿着x轴正方向做直线运动.其位移随时间的变化规律为x = 6.0 t -10 t 2.式中x的单位为m.t的单位为s.不计空气阻力.取g =10m/s2. 【查看更多】

在水平面内的直角体系xOy中有一光滑金属导轨AOC，其中曲线导轨OA满足方程y=Lsinkx，长度为

的直导轨OC与x轴重合，整个导轨处于竖直向上的匀强磁场中，其俯视图如图所示。现有一长为L的金属棒从图示位置开始沿x轴正方向做匀速直线运动，已知金属棒单位长度的电阻值为R₀，除金属棒的电阻外其余电阻均不计，棒与两导轨始终接触良好，则在金属棒运动的过程中

[ ]

A．回路中的感应电动势保持不变
B．回路中的感应电流保持不变
C．回路中消耗的电功率保持不变
D．金属棒所受的安培力保持不变

查看答案和解析>>

（18分）在竖直平面内建立一平面直角坐标系xoy，x轴沿水平方向，如图甲所示。第一象限内有竖直向上的匀强电场，第二象限内有一水平向右的匀强电场。某种发射装置（未画出）竖直向上发射出一个质量为m、电荷量为q的带正电粒子（可视为质点），该粒子以v₀的初速度从x轴上的A点进入第二象限，并从y轴上的C点沿水平方向进入第一象限后能够沿水平方向运动到D点。已知OA、OC距离相等，CD的距离为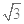OC，E点在D点正下方，位于x轴上，重力加速度为g。则：

（1）求粒子在C点的速度大小以及OC之间的距离；

（2）若第一象限同时存在按如图乙所示规律变化的磁场，磁场方向垂直纸面，（以垂直纸面向外的磁场方向为正方向，图中B₀，T₀均为未知量），并且在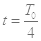时刻粒子由C点进入第一象限，且恰好也能通过同一水平线上的D点，速度方向仍然水平。若粒子在第一象限中运动的周期与磁场变化周期相同，求交变磁场变化的周期；

（3）若第一象限仍同时存在按如图乙所示规律变化的磁场（以垂直纸面向外的磁场方向为正方向，图中B₀，T₀均为未知量），调整图乙中磁场变化的周期，让粒子在t=0时刻由C点进入第一象限，且恰能通过E点，求交变磁场的磁感应强度B₀应满足的条件。

查看答案和解析>>

在竖直平面内，一根光滑金属杆弯成如图所示形状，相应的曲线方程为y＝2．5cos（kx＋π）（单位：m），式中k＝1m^－1。将一光滑小环套在该金属杆上，开始时小环静止于金属杆的最低点，给小环以v₀＝10m/s的水平初速度沿杆向右运动。取重力加速度g＝10m/s²，关于小环的运动，下列说法正确的是（）

A．金属杆对小环不做功

B．小环沿x轴方向的分运动为匀速运动

C．小环能到达金属杆的最高点

D．小环不能到达金属杆的最高点

查看答案和解析>>

（18分）在竖直平面内建立一平面直角坐标系xoy，x轴沿水平方向，如图甲所示。第一象限内有竖直向上的匀强电场，第二象限内有一水平向右的匀强电场。某种发射装置（未画出）竖直向上发射出一个质量为m、电荷量为q的带正电粒子（可视为质点），该粒子以v₀的初速度从x轴上的A点进入第二象限，并从y轴上的C点沿水平方向进入第一象限后能够沿水平方向运动到D点。已知OA、OC距离相等，CD的距离为OC，E点在D点正下方，位于x轴上，重力加速度为g。则：

（1）求粒子在C点的速度大小以及OC之间的距离；
（2）若第一象限同时存在按如图乙所示规律变化的磁场，磁场方向垂直纸面，（以垂直纸面向外的磁场方向为正方向，图中B₀，T₀均为未知量），并且在时刻粒子由C点进入第一象限，且恰好也能通过同一水平线上的D点，速度方向仍然水平。若粒子在第一象限中运动的周期与磁场变化周期相同，求交变磁场变化的周期；
（3）若第一象限仍同时存在按如图乙所示规律变化的磁场（以垂直纸面向外的磁场方向为正方向，图中B₀，T₀均为未知量），调整图乙中磁场变化的周期，让粒子在t=0时刻由C点进入第一象限，且恰能通过E点，求交变磁场的磁感应强度B₀应满足的条件。

查看答案和解析>>

（18分）在竖直平面内建立一平面直角坐标系xoy，x轴沿水平方向，如图甲所示。第一象限内有竖直向上的匀强电场，第二象限内有一水平向右的匀强电场。某种发射装置（未画出）竖直向上发射出一个质量为m、电荷量为q的带正电粒子（可视为质点），该粒子以v₀的初速度从x轴上的A点进入第二象限，并从y轴上的C点沿水平方向进入第一象限后能够沿水平方向运动到D点。已知OA、OC距离相等，CD的距离为

OC，E点在D点正下方，位于x轴上，重力加速度为g。则：

（1）求粒子在C点的速度大小以及OC之间的距离；
（2）若第一象限同时存在按如图乙所示规律变化的磁场，磁场方向垂直纸面，（以垂直纸面向外的磁场方向为正方向，图中B₀，T₀均为未知量），并且在

时刻粒子由C点进入第一象限，且恰好也能通过同一水平线上的D点，速度方向仍然水平。若粒子在第一象限中运动的周期与磁场变化周期相同，求交变磁场变化的周期；
（3）若第一象限仍同时存在按如图乙所示规律变化的磁场（以垂直纸面向外的磁场方向为正方向，图中B₀，T₀均为未知量），调整图乙中磁场变化的周期，让粒子在t=0时刻由C点进入第一象限，且恰能通过E点，求交变磁场的磁感应强度B₀应满足的条件。

查看答案和解析>>

一、1、C 2、B 3、C 4、C 5、C 6、C 7、D 8、ACD

二、实验题：（18分）将答案填在题目的空白处，或者要画图连线。

9、（9分）①（2分）P

②（3分）3.66×10^-3(或3.7×10^-3); 0.54%

在实验误差允许范围内，可认为系统在碰前的动量和碰后的支量是相等的。

③（2分）D

④（2分）