
题目列表(包括答案和解析)
若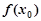 是函数
是函数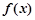 在点
在点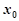 附近的某个局部范围内的最大(小)值,则称
附近的某个局部范围内的最大(小)值,则称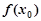 是函数
是函数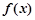 的一个极值,
的一个极值,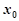 为极值点.已知
为极值点.已知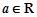 ,函数
,函数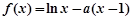 .
.
(Ⅰ)若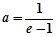 ,求函数
,求函数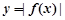 的极值点;
的极值点;
(Ⅱ)若不等式 恒成立,求
恒成立,求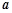 的取值范围.
的取值范围.
(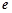 为自然对数的底数)
为自然对数的底数)
若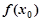 是函数
是函数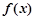 在点
在点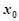 附近的某个局部范围内的最大(小)值,则称
附近的某个局部范围内的最大(小)值,则称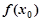 是函数
是函数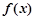 的一个极值,
的一个极值,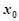 为极值点.已知
为极值点.已知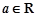 ,函数
,函数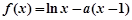 .
.
(Ⅰ)若 ,求函数
,求函数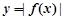 的极值点;
的极值点;
(Ⅱ)若不等式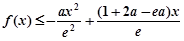 恒成立,求
恒成立,求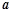 的取值范围.
的取值范围.
(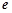 为自然对数的底数)
为自然对数的底数)
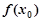 是函数
是函数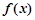 在点
在点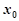 附近的某个局部范围内的最大(小)值,则称
附近的某个局部范围内的最大(小)值,则称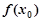 是函数
是函数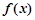 的一个极值,
的一个极值,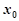 为极值点.已知
为极值点.已知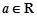 ,函数
,函数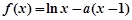 .
.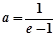 ,求函数
,求函数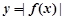 的极值点;
的极值点;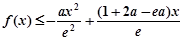 恒成立,求
恒成立,求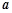 的取值范围.
的取值范围.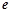 为自然对数的底数)
为自然对数的底数)()某地2004年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下:
| 行业名称 | 计算机 | 机械 | 营销 | 物流 | 贸易 |
| 应聘人数 | 215830 | 200250 | 154676 | 74570 | 65280 |
| 行业名称 | 计算机 | 营销 | 机械 | 建筑 | 化工 |
| 招聘人数 | 124620 | 102935 | 89115 | 76516 | 70436 |
若用同一行业中应聘人数与招聘人数比值的大小来衡量该行业的就业情况,则根据表中的数据,就业形势一定是 ( )
A.计算机行业好于化工行业 B.建筑行业好于物流行业
C.机械行业最紧张 D.营销行业比贸易行业紧张
16、某地2004年第一季度应聘和招聘人数排行榜前5个行业的情况列表如下
|
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
D
A
B
D
B
C
B
C
D
B
1.提示: 所以
所以 ,故选C。
,故选C。
2.提示:命题P: ,所以命题P是假命题,
,所以命题P是假命题,
命题Q

当 时,。
时,。  ,所以以命题Q是真命题,故选D。故选A。
,所以以命题Q是真命题,故选D。故选A。
3.提示: 又
又 ,所以
,所以 ,故选D。
,故选D。
4.提示:在AB上取点D,使得 ,则点P只能在AD内运动,则
,则点P只能在AD内运动,则 ,
,
5.提示: 故选B。
故选B。
6.提示:由图(1)改为图(2)后每次循环时 的值都为1,因此运行过程出现无限循环,故选D
的值都为1,因此运行过程出现无限循环,故选D
7.提示:设全班40个人的总分为S,
则 ,故选B。
,故选B。
8.提示:
所以约束条件为 表示的平面区域是以点O(0,0),
表示的平面区域是以点O(0,0), ,N(0,1),Q(2,3)为顶点的平行四边形(包括边界),故当
,N(0,1),Q(2,3)为顶点的平行四边形(包括边界),故当 时,
时, 的最大值是4,故选C。
的最大值是4,故选C。
 9.提示:由
9.提示:由 及
及 得
得
 如图
如图
过A作 于M,则
于M,则



 得
得 .
.
故选B.
10.提示:不妨设点(2,0)与曲线 上不同的三的点距离为分别
上不同的三的点距离为分别 ,它们组成的等比数列的公比为
,它们组成的等比数列的公比为 若令
若令 ,显然
,显然 ,又
,又 所以
所以 ,
, 不能取到
不能取到 。故选B。
。故选B。
11.提示:使用特值法:取集合 当
当 可以排除A、B;
可以排除A、B;
取集合 ,当
,当 可以排除C;故选D;
可以排除C;故选D;
12.提示:n棱柱有 个顶点,被平面截去一个三棱锥后,可以分以下6种情形(图1~6)
个顶点,被平面截去一个三棱锥后,可以分以下6种情形(图1~6)






在图4,图6所示的情形,还剩 个顶点;
个顶点;
在图5的情形,还剩 个顶点;
个顶点;
在图2,图3的情形,还剩 个顶点;
个顶点;
在图1的情形,还剩下 个顶点.故选B.
个顶点.故选B.
二、填空题:
13.
提示:由
14.
提示:斜率 ,切点
,切点 ,所以切线方程为:
,所以切线方程为:
15.
提示:当 时,不等式无解,当
时,不等式无解,当 时,不等式变为
时,不等式变为 ,
,
由题意得 或
或 ,所以,
,所以, 或
或
16.
三、解答题:
17.解:① ∵ ∴
∴ 的定义域为R;
的定义域为R;
② ∵ ,
,
∴ 为偶函数;
为偶函数;
③ ∵ , ∴
, ∴ 是周期为
是周期为 的周期函数;
的周期函数;
④ 当 时,
时, =
= ,
,
∴当 时
时 单调递减;当
单调递减;当 时,
时,
 =
= ,
,
 单调递增;又∵
单调递增;又∵ 是周期为
是周期为 的偶函数,∴
的偶函数,∴ 在
在 上单调递增,在
上单调递增,在 上单调递减(
上单调递减( );
);
⑤ ∵当 时
时 ;
;
当 时
时 .∴
.∴ 的值域为
的值域为 ;
;
⑥由以上性质可得: 在
在 上的图象如图所示:
上的图象如图所示:

18.解:(Ⅰ)取PC的中点G,连结EG,GD,则
由(Ⅰ)知FD⊥平面PDC, 面PDC,所以FD⊥DG。
面PDC,所以FD⊥DG。
所以四边形FEGD为矩形,因为G为等腰Rt△RPD斜边PC的中点,
所以DG⊥PC,
|