
题目列表(包括答案和解析)
在计算“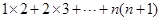 ”时,先改写第k项:
”时,先改写第k项:
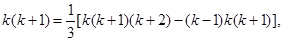 由此得
由此得
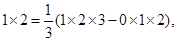
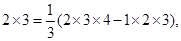 ……
……
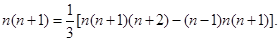
相加,得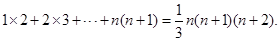
(1)类比上述方法,请你计算“ ”的结果;
”的结果;
(2) 试用数学归纳法证明你得到的等式.
在计算“1×2+2×3+...+n(n+1)”时,某同学学到了如下一种方法:
先改写第k项:k(k+1)=
由此得1×2= .
. .
.
............. .
.
相加,得1×2+2×3+...+n(n+1) .
.
类比上述方法,请你计算“1×2×3×4+2×3×4×+....+ ”,其结果是_________________.(结果写出关于
”,其结果是_________________.(结果写出关于 的一次因式的积的形式)
的一次因式的积的形式)
在计算“1×2+2×3+...+n(n+1)”时,某同学学到了如下一种方法:
先改写第k项:k(k+1)=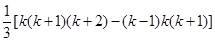
由此得1×2-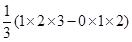 .
.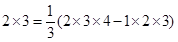 .
.
.............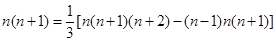 .
.
相加,得1×2+2×3+...+n(n+1)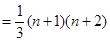 .
.
类比上述方法,请你计算“1×2×3×4+2×3×4×+....+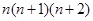 ”,
”,
其结果是_________________.(结果写出关于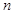 的一次因式的积的形式)
的一次因式的积的形式)
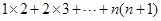 ”时,先改写第k项:
”时,先改写第k项: 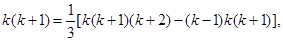 由此得
由此得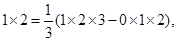
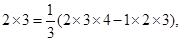 ……
……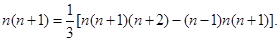
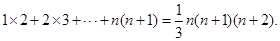
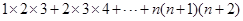 ”的结果;
”的结果; [k(k+1)(k+2)-(k-1)k(k+1)],由此得1×2=
[k(k+1)(k+2)-(k-1)k(k+1)],由此得1×2= (1×2×3-0×1×2),2×3=
(1×2×3-0×1×2),2×3= (2×3×4-1×2×3),..
(2×3×4-1×2×3),.. [n(n+1)(n+2)-(n-1)n(n+1)],相加,得1×2+2×3+…+n(n+1)=
[n(n+1)(n+2)-(n-1)n(n+1)],相加,得1×2+2×3+…+n(n+1)=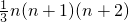
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com