
题目列表(包括答案和解析)
| 第一列 | 第二列 | 第三列 | |
| 第一行 | -3 | 3 | 1 |
| 第二行 | 5 | 0 | 2 |
| 第三行 | -1 | 2 | 0 |
| an+2 |
| 2n |
| 第一列 | 第二列 | 第三列 | |
| 第一行 | -3 | 3 | 1 |
| 第二行 | 5 | 0 | 2 |
| 第三行 | -1 | 2 | 0 |
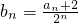 ,设数列{bn}的前n项和Sn(n∈N*),证明:Sn<2.
,设数列{bn}的前n项和Sn(n∈N*),证明:Sn<2. 满足
满足 ,
, 。
。 、
、 、
、 ;
; 是公差为-1的等差数列,若存在求出t的值,否则,请说明理由;
是公差为-1的等差数列,若存在求出t的值,否则,请说明理由; ,数列
,数列 的前n项和为Sn,求证:
的前n项和为Sn,求证: 。
。  ,并求数列{cn}的前n项和Tn;
,并求数列{cn}的前n项和Tn; 是公差为8的准等差数列.
是公差为8的准等差数列.一、选择题:
1.D 2.A 3 B 4.D 5.A 6.D 7.B 8.C 9.A 10.B 11.A 12.B
二、填空题:
13.12 14. 15 3 16.,①②③④
15 3 16.,①②③④
三、解答题:
17.解:法(1):①∵ =(1+cosB,sinB)与
=(1+cosB,sinB)与 =(0,1)所成的角为
=(0,1)所成的角为
∴ 与向量
与向量 =(1,0)所成的角为
=(1,0)所成的角为
∴ ,即
,即 (2分)
(2分)
而B∈(0,π),∴ ,∴
,∴ ,∴B=
,∴B= 。 (4分)
。 (4分)
②令AB=c,BC=a,AC=b
∵B= ,∴b2=a2+c2-2accosB=a2+c2-ac=
,∴b2=a2+c2-2accosB=a2+c2-ac= ,∵a,c>0。
(6分)
,∵a,c>0。
(6分)
∴a2+c2≥ ,ac≤
,ac≤ (当且仅当a=c时等号成立)
(当且仅当a=c时等号成立)
∴12=a2+c2-ac≥
 (8分)
(8分)
∴(a+c)2≤48,∴a+c≤ ,∴a+b+c≤
,∴a+b+c≤ +
+ =
= (当且仅当a=c时取等号)
(当且仅当a=c时取等号)
故ΔABC的周长的最大值为 。 (10分)
。 (10分)
法2:(1)cos< ,
, >=cos
>=cos
∴ , (2分)
, (2分)
即2cos2B+cosB-1=0,∴cosB= 或cosB=-1(舍),而B∈(0,π),∴B=
或cosB=-1(舍),而B∈(0,π),∴B= (4分)
(4分)
(2)令AB=c,BC=a,AC=b,ΔABC的周长为 ,则
,则 =a+c+
=a+c+
而a=b? ,c=b?
,c=b? (2分)
(2分)
∴ =
= =
=
= (8分)
(8分)
∵A∈(0, ),∴A-
),∴A- ,
,
当且仅当A= 时,
时, 。
(10分)
。
(10分)
18.解法一:(1)∵PA⊥底面ABCD,BC 平面AC,∴PA⊥BC
平面AC,∴PA⊥BC
∵∠ACB=90°,∴BC⊥AC,又PA∩AC=A,∴BC⊥平面PAC
(2)∵AB∥CD,∠BAD=120°,∴∠ADC=60°,又AD=CD=1
∴ΔADC为等边三角形,且AC=1,取AC的中点O,则DO⊥AC,又PA⊥底面ABCD,
∴PA⊥DO,∴DO⊥平面PAC,过O作OH⊥PC,垂足为H,连DH
由三垂成定理知DH⊥PC,∴∠DHO为二面角D-PC-A的平面角
由OH= ,DO=
,DO= ,∴tan∠DHO=
,∴tan∠DHO= =2
=2
∴二面角D-PC-A的大小的正切值为2。
 (3)设点B到平面PCD的距离为d,又AB∥平面PCD
(3)设点B到平面PCD的距离为d,又AB∥平面PCD
∴VA-PCD=VP-ACD,即
∴ 即点B到平面PCD的距离为
即点B到平面PCD的距离为 。
。
19.解:(1)第一和第三次取球对第四次无影响,计第四次摸红球为事件A
①第二次摸红球,则第四次摸球时袋中有4红球概率为
 (2分)
(2分)
②第二次摸白球,则第四次摸球时袋中有5红2白,摸红球概率为
 (3分)
(3分)
∴P(A)= ,即第四次恰好摸到红球的概率为
,即第四次恰好摸到红球的概率为 。(6分)(注:无文字说明扣一分)
。(6分)(注:无文字说明扣一分)
(2)由题设可知ξ的所有可能取值为:ξ=0,1,2,3。P(ξ=0)= ;
;
P(ξ=1)= ;P(ξ=2)=
;P(ξ=2)= ;
;
P(ξ=3)= 。故随机变量ξ的分布列为:
。故随机变量ξ的分布列为:
ξ
0
1
2
|