
题目列表(包括答案和解析)
(本大题满分14分)
已知数列 和
和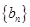 满足:
满足: ,
, ,
,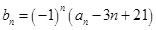 ,其中
,其中 为实数,
为实数, 为正整数.
为正整数.
(Ⅰ)对任意实数 ,证明:数列
,证明:数列 不是等比数列;
不是等比数列;
(Ⅱ)证明:当 时,数列
时,数列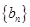 是等比数列;
是等比数列;
(Ⅲ)设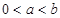 (
( 为实常数),
为实常数),  为数列
为数列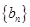 的前
的前 项和.是否存在实数
项和.是否存在实数 ,使得对任意正整数
,使得对任意正整数 ,都有
,都有 ?若存在,求
?若存在,求 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
(本大题满分14分)
设函数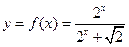 上两点
上两点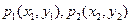 ,若
,若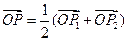 ,且P点的横坐标为
,且P点的横坐标为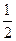 .
.
(1)求P点的纵坐 标;
标;
(2)若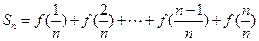 求
求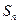 ;
;
(3)记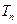 为数列
为数列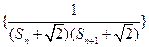 的前n项和,若
的前n项和,若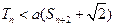 对一切
对一切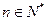 都成立,试求a的取值范围.
都成立,试求a的取值范围.
(本大题满分14分)
已知数列{an}的前n项和Sn是二项式![]() 展开式中含x奇次幂的系数和.
展开式中含x奇次幂的系数和.
(1)求数列{an}的通项公式;
(2)设![]() ,求
,求![]() ;
;
(3)证明:![]() .
.
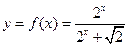 上两点
上两点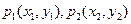 ,若
,若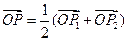 ,且P点的横坐标为
,且P点的横坐标为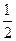 .
. 标;
标;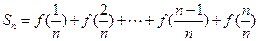 求
求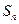 ;
;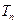 为数列
为数列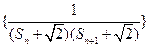 的前n项和,若
的前n项和,若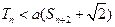 对一切
对一切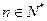 都成立,试求a的取值范围.
都成立,试求a的取值范围. (本大题满分14分)
已知关于x的不等式![]() 的解集为A,且
的解集为A,且![]()
(1)求实数![]() 的取值范围;
的取值范围;
(2)并用![]() 表示出该不等式的解集A.
表示出该不等式的解集A.
一.1、A,2、C,3、B,4、D,5、C,6、B,7、A,8、C,9、A,10、D
二.11、-3;.12、1;13、 14、
14、 15、
15、
三.16.解:
 ……(2’)
……(2’)
整理得: ……………………………(4’)
……………………………(4’)
又A为锐角, …………………(6’)
…………………(6’)
(2)由(1)知 ………………………(7’)
………………………(7’)
故

……………………………(12’)
当B=600时,Y取得最大值。……………………(13’)
17. 设答对题的个数为y,得分为 ,y=0,1,2,4 ,
,y=0,1,2,4 , =0,2,4,8………(1’)
=0,2,4,8………(1’)
∵ ,
,
 ,
,
|