练习册

  • 练习册
  • 试题
    交点个数为 ． 【查看更多】

     

    题目列表(包括答案和解析)

    5、为了考察两个变量x、y之间的线性相关关系，甲、乙两同学各自独立地做10次和15次试验，并利用最小二乘法求得回归直线分别为l1和l2．已知在两人的试验中发现变量x的观测数据的平均值恰好都为s，变量y的观测数据的平均值恰好都为t，那么下列说法中正确的有（　　）

    查看答案和解析>>

    10、为了考察两个变量之间是否存在着线性相关性，天成和冰叶两人各自独立地做了20次和30次试验，并且利用所学知识，分别求得回归直线方程l1和l2，已知两人所得变量x数据的平均数都为a，所得变量y数据的平均数都为b．则下列说法正确的是（　　）

    查看答案和解析>>

    为进行科学实验，观测小球A、B在两条相交成60°角的直线型轨道上运动的情况，如图所示，运动开始前，A和B分别距O点3m和1m，后来它们同时以每分钟4m的速度各沿轨道l1、l2按箭头的方向运动．问：
    （1）运动开始前，A、B的距离是多少米？（结果保留三位有效数字）．
    （2）几分钟后，两个小球的距离最小？

    查看答案和解析>>

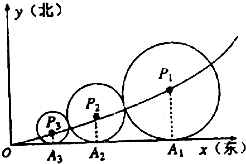    为建设好长、株、潭“两型社会”改革实验区，加快二市经济一体化进程，某规划部门在三市的交界处拟建一个大型环保生态公园，并在公园入口处的东南方位建造一个供市民休闲健身的小型绿化广场，如图是步行小道设计方案示意图，其中，Ox，Oy分别表示自西向东，自南向北的两条主干道，设计方案是自主干道交汇点O处修一条步行小道，小道为抛物线y=x2的一段，在小道上依次以点P1(x1，y1)，P2(x2，y2)，…，P(xn，yn)(n≥10，n∈N*)为圆心，修一系列圆型小道，且这些圆型小道与主干道Ox分别于相切于A1，A2，…，An，…，且任意相邻的两圆彼此外切，若x1=1（单位：百米），且xn+1＜xn．
    （1）记⊙P1，⊙P2，…，⊙Pn，…的半径rn组成的数列为{rn}，求通项公式rn；
    （2）若修建这些圆形小道工程预算总费用为50万元，根据以往施工经验可知，面积为S的圆形小道的实际施工费用为10
    		πS
    万元，试问修建好前n（n≥10，n∈N*）个圆型小道，预算费用是否够用，请说明你的理由．

    查看答案和解析>>

    点Q在x轴上，若存在过Q的直线交函数y=2x的图象于A，B两点，满足
    QA
    =
    AB
    ，则称点Q为“Ω点”，那么下列结论中正确的是（　　）

    查看答案和解析>>

    一．选择题 (本大题共10小题，每题5分，共50分)

    1．C；    2．D；    3，A；    4．B；     5．B；

    6．B；    7．B；    8．B；    9．D；     10．B；

    二．填空题 (本大题共7小题，每题4分，共28分)

    11．；  12．； ．；   14．，；  15．；  16．；  17．．

    三．解答题 (本大题共5小题，第18―20题各14分，第21、22题各15分，共72分)

    18．解：(1)因为，所以，得…………3分

        又因为…………………………………3分

    （2）由及，得，…………………………………2分

        所以，…………………………………2分

        ，…………………………………2分

        ………………………………2分

    19．如图建立空间直角坐标系，                  

     则，，

    ……………………1分

        （1），………………1分

            ，……………………1分

            ……………………1分

          ∴，……2分

         又与相交，所以平面……1分

    (2)设平面的一个法向量为，

    因为，所以可取…………………………………………………2分

    又平面的一个法向量为……………………………………………2分

    ∴  …………………………2分

    ∴二面角的大小为……………………………………………1分

    20．解：(1)抛一次骰子面朝下的点数有l、2、3、4四种情况，

    而点数大于2的有2种，故闯第一关成功的概率……………………2分

    （2）记事件“抛掷次骰子，各次面朝下的点数之和大于”为事件，

    则，

    抛二次骰子面朝下的点数和

    情况如右图所示，

    故…………………………………………2分

    抛三次骰子面朝下的点数依次记为：，，

    考虑的情况

    时，有1种，时，有3种

    时，有6种，时，有10种

    故……………………………4分

    由题意知可取0、1、2、3，

    ，………………………1分

    ，………………………1分

    ，………………………1分

    ，………………………1分

    ∴的分布列为：

     

     

     

       ……………………2分

    21．(1)法一：由已知………………………………1分

        设，则，……………………………1分

        ，………………………1分

        由得，，

    解得………………………2分

    法二：记A点到准线距离为，直线的倾斜角为，

    由抛物线的定义知，………………………2分

    ∴，

    ∴………………………3分

    （2）设，，

    由得，………………………1分

    首先由得且

    ，同理……………………2分

    由得，…………………………2分

    即：，

        ∴，…………………………2分

    ，得且，

    由且得，

    的取值范围为…………………………3分

    22．（1）时，，

    ，，………………………2分

    又

    所以切线方程为………………………2分

    （2）1°当时，，则

    令，，

    再令，

    当时，∴在上递减，

    ∴当时，，

    ∴，所以在上递增，，

    所以……………………5分

    2°时，，则

    由1°知当时，在上递增

    当时，，

    所以在上递增，∴

    ∴；………………………5分

    由1°及2°得：………………………1分

     

     

    命题人

    吕峰波(嘉兴)、 王书朝(嘉善)、 王云林(平湖)

    胡水林(海盐)、 顾贯石(海宁)、  张晓东(桐乡)

         吴明华、张启源、徐连根、洗顺良、李富强、吴林华

     


    同步练习册答案