
题目列表(包括答案和解析)
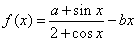 (a、b∈R),
(a、b∈R),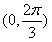 为增函数,
为增函数,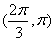 为减函数,若存在,求出b的值,若不存在,请说明理由;
为减函数,若存在,求出b的值,若不存在,请说明理由;己知常数a、b都是实数,f(x)=![]() x3+
x3+![]() ax2+bx-5,直线l的方程为6x+3y-19=0.
ax2+bx-5,直线l的方程为6x+3y-19=0.
(Ⅰ)如果f(x)在实数集R上是单调函数,求a、b满足的条件;
(Ⅱ)设点(1,f(1))、(2,f(2))是f(x)的两个极值点,问:y=f(x)的图象上是否存在与直线l平行的切线?如果存在,求出直线l平行的切线的方程;如果不存在,请说明理由.
| π |
| 2 |
| Sn |
| n |
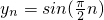 时,{yn}的周期为4的周期数列.
时,{yn}的周期为4的周期数列.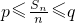 成立,若存在,求出p、q的取值范围;不存在,说明理由.
成立,若存在,求出p、q的取值范围;不存在,说明理由.| π |
| 2 |
| Sn |
| n |
一、选择题
1、C
9、B 先从8人中选3人有全真模拟试题(三)09-3.files/image212.gif) 种方法,选出的3人调换座位有
种方法,选出的3人调换座位有全真模拟试题(三)09-3.files/image214.gif) 种调换方式共有
种调换方式共有全真模拟试题(三)09-3.files/image212.gif)
全真模拟试题(三)09-3.files/image214.gif) =112种。
=112种。
二、填空题
15、 ②⑤ 由对称性可知,所得图形应为中心对称图形②⑤截得。
三、解答题
18、(1)以DA、DC、DP所在直线分别为全真模拟试题(三)09-3.files/image283.gif) 建立空间直角坐标系
建立空间直角坐标系
19、(1)面上是数字0的概率为全真模拟试题(三)09-3.files/image301.gif) ,数字为1的概率为
,数字为1的概率为全真模拟试题(三)09-3.files/image303.gif) ,数学为2的概率为
,数学为2的概率为全真模拟试题(三)09-3.files/image305.gif) ,当甲掷出的数字为1,乙掷出的数字为0时,甲获胜的概率为
,当甲掷出的数字为1,乙掷出的数字为0时,甲获胜的概率为全真模拟试题(三)09-3.files/image307.gif) 当甲掷出的数字为2,乙掷出的数字为0或1时,甲获胜的概率为
当甲掷出的数字为2,乙掷出的数字为0或1时,甲获胜的概率为全真模拟试题(三)09-3.files/image309.gif)
0
1
2
4
-
0
+
ㄋ
极小值
ㄊ
+
0
-
0
+
ㄊ
极大值
ㄋ
极小值
ㄊ
『每一套试卷、教案或教学设计等教学素材不仅是知识的生动展现,更是都是作者整理、编辑这部分资料的时候心血和智慧与创造力的结晶!与此同时,为了适应新课程改革和学生科学素质的发展的需要,我们在尊重元资料的基础上,更注重对选材的代表性和借鉴性的挑剔,注重与对学生基础知识、基本技能和创新能力培养的结合――我们唯一的目的:它山之石,可以攻玉;为祖国的教育事业尽到责任!!!――柳垭职业中学』
本资料由《七彩教育网》www.7caiedu.cn 提供!
本资料来源于《七彩教育网》http://www.7caiedu.cn
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com