
题目列表(包括答案和解析)
数学命题推理有合情推理和演绎推理,________和________是常用的合情推理.从推理形式上看,________是由部分到整体,个别到一般的推理,________是由特殊到特殊的推理,而演绎推理是由一般到特殊的推理;从推理所得的结论来看,________的结论不一定正确,有待于进一步证明,________在前提和推理形式都正确的前提下,得到的结论一定正确.
函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 。
。
(1)求实数a,b,并确定函数 的解析式;
的解析式;
(2)判断 在(-1,1)上的单调性,并用定义证明你的结论;
在(-1,1)上的单调性,并用定义证明你的结论;
(3)写出 的单调减区间,并判断
的单调减区间,并判断 有无最大值或最小值?如有,写出最大值或最小值。(本小问不需要说明理由)
有无最大值或最小值?如有,写出最大值或最小值。(本小问不需要说明理由)
【解析】本试题主要考查了函数的解析式和奇偶性和单调性的综合运用。第一问中,利用函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 。
。
解得 ,
,
(2)中,利用单调性的定义,作差变形判定可得单调递增函数。
(3)中,由2知,单调减区间为 ,并由此得到当,x=-1时,
,并由此得到当,x=-1时, ,当x=1时,
,当x=1时,
解:(1) 是奇函数,
是奇函数, 。
。
即 ,
, ,
, ………………2分
………………2分
 ,又
,又 ,
, ,
, ,
,
(2)任取 ,且
,且 ,
,
 ,………………6分
,………………6分
 ,
,
 ,
, ,
, ,
, ,
,
 在(-1,1)上是增函数。…………………………………………8分
在(-1,1)上是增函数。…………………………………………8分
(3)单调减区间为 …………………………………………10分
…………………………………………10分
当,x=-1时, ,当x=1时,
,当x=1时, 。
。
正方形ABCD中,点O是对角线AC的中点,点P是对角线AC上一动点.
(1)如图1,当点P在线段OA上运动时(不与点A、O重合) ,PE⊥PB交线段CD于点E,PF⊥CD于点E.

①判断线段DF、EF的数量关系,并说明理由;
②写出线段PC、PA、CE之间的一个等量关系,并证明你的结论;
(2)如图2,当点P在线段OC上运动时(不与点O、C重合),PE⊥PB交直线CD于点E,PF⊥CD于点E.判断(1)中的结论①、②是否成立?若成立,说明理由;若不成立,写出相应的结论并证明.
设函数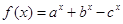 ,其中
,其中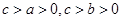 .
.
(1)记集合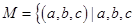 不能构成一个三角形的三边长,且
不能构成一个三角形的三边长,且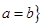 ,则
,则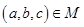 所对应的
所对应的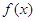 的零点的取值集合为 ;
的零点的取值集合为 ;
(2)若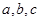 是
是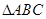 的三边长,则下列结论正确的是 (写出所有正确结论的序号).
的三边长,则下列结论正确的是 (写出所有正确结论的序号).
①对于区间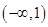 内的任意
内的任意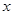 ,总有
,总有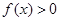 成立;
成立;
②存在实数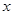 ,使得
,使得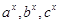 不能同时成为任意一个三角形的三条边长;
不能同时成为任意一个三角形的三条边长;
③若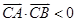 ,则存在实数
,则存在实数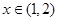 ,使
,使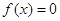 .(提示 :
.(提示 :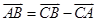 )
)
(第(1)空2分,第(2)空3分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com