练习册

  • 练习册
  • 试题
    18． (理)袋中有编号为1.2.3.4的四个小球.每次从袋中取出一个球.然后加入一个新的没有编号的球.共取球四次.用ξ表示经过四次取球后袋中剩余的带有编号的球的个数.试求: (1)ξ的分布列, (2)ξ的数学期望Eξ. (文)袋中有编号为1.2.3.4的四个小球.每次从袋中取出一个球.然后加入一个新的没有编号的球.共取球四次.试求: (1)经过四次取球后袋中没有带有编号的球的概率, (2)经过四次取球后袋中至少有2个带有编号的球的概率. 【查看更多】

     

    题目列表(包括答案和解析)

    （本小题满分12分）

    （理）袋中有同样的球5个，其中3个红色，2个黄色，现从中随机且不放回地摸球，每次摸1个，当两种颜色的球都被摸到时，即停止摸球，记随机变量ξ为此时已摸球的次数，求：

    (1)随机变量ξ的概率分布； (9分) 

    (2)随机变量ξ的数学期望与方差. （3分）

    查看答案和解析>>

    （本小题满分12分）口袋里装有大小相同的卡片八张，其中三张标有数字1，三张标有数字2，二张标有数字3，第一次从口袋里任意抽取一张，放回口袋后第二次再任意抽取一张，记第一次与第二次取到卡片上数字之和为ξ.(1)ξ为何值时，其发生的概率最大？说明理由.(2)求随机变量ξ的期望Eξ.

    查看答案和解析>>

    （本小题满分12分）袋子中有质地、大小完全相同的4个球，编号分别为1，2，3，4．甲、乙两人玩一种游戏：甲先摸出一个球，记下编号，放回后乙再摸一个球，记下编号，若两个编号的和为奇数算甲赢，否则算乙赢．记基本事件为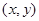，其中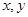分别为甲、乙摸到的球的编号。

    （1）列举出所有的基本事件，并求甲赢且编号的和为5的事件发生的概率；

    （2）比较甲胜的概率与乙胜的概率，并说明这种游戏规则是否公平。（无详细解答过程，不给分）

    （3）   如果请你猜这两球的号码之和，猜中有奖．猜什么数获奖的可能性大？说明理由．

     

    查看答案和解析>>

    （本小题满分12分）

    口袋里装有大小相同的卡片八张，其中三张标有数字1，三张标有数学2，二张标有数字3，第一次从口袋里任里任意抽取一张，放回口袋里后第二次再任意抽取一张，记第一次与第二次取到卡片上数字这和为

       （Ⅰ）为何值时，其发生的概率最大？说明理由；

       （Ⅱ）求随机变量的期望

    查看答案和解析>>

    （本小题满分12分）袋子中有质地、大小完全相同的4个球，编号分别为1，2，3，4．甲、乙两人玩一种游戏：甲先摸出一个球，记下编号，放回后乙再摸一个球，记下编号，若两个编号的和为奇数算甲赢，否则算乙赢．记基本事件为，其中分别为甲、乙摸到的球的编号。
    （1）列举出所有的基本事件，并求甲赢且编号的和为5的事件发生的概率；
    （2）比较甲胜的概率与乙胜的概率，并说明这种游戏规则是否公平。（无详细解答过程，不给分）
    （3）  如果请你猜这两球的号码之和，猜中有奖．猜什么数获奖的可能性大？说明理由．

    查看答案和解析>>

     

    一、选择题

    1―5 CADBA    6―10 CBABD    11―12 CC

    二、填空题

    13．（理）（文）（―1，1）    14．    15．（理）18（文）（1，0）

    16．①③

    三、解答题

    17．解：（1）由题意得   ………………2分

       

       （2）由可知A、B都是锐角，   …………7分

       

        这时三角形为有一顶角为120°的等腰三角形   …………12分

    18．（理）解：（1）ξ的所有可能的取值为0，1，2，3。  ………………2分

       

       （2）   ………………12分

       （文）解：（1）；  ………………6分

       （2）因为

          …………10分

        所以   …………12分

    19．解：（1），   ………………1分

        依题意知，   ………………3分

       （2）令   …………4分

         …………5分

        所以，…………7分

       （3）由上可知

        ①当恒成立，

        必须且只须， …………8分

        ，

         则   ………………9分

        ②当……10分

        要使当

        综上所述，t的取值范围是   ………………12分

    20．解法一：（1）取BB1的中点D，连CD、AD，则∠ACD为所求。…………1分

       

       （2）方法一 作CE⊥AB于E，C1E1⊥A1B1于E1，连EE1，

    则AB⊥面CC1E1E，因此平面PAB⊥面CC1E1E。

    因为A1B1//AB，所以A1B1//平面PAB。则只需求点E1到平面PAB的距离。

    作E1H⊥EP于H，则E1H⊥平面PAB，则E1H即为所求距离。  …………6分

    求得 …………8分

    方法二：设B1到平面PAB的距离为h，则由

    得  ………………8分

       （3）设平面PAB与平面PA1B1的交线为l，由（2）知，A1B1//平面PAB，

    则A1B1//l，因为AB⊥面CC1E1E，则l⊥面CC1E1E，

    所以∠EPE1就是二面有AB―P―A1B的平面角。 ………………9分

    要使平面PAB⊥平面PA1B1，只需∠EPE1=90°。  ………………10分

    在矩形CEE1C1中，

    解得

    解法二：（1）取B1C1的中点O，则A1O⊥B1C1，

    以O为坐标原点，建立空间直角坐标系如图，

       （2）是平面PAB的一个法向量，

       ………………5分

    令   ………………6分

    又  ………………8分

       （3）设P点坐标为（），则

    设是平面PAB的一个法向量，与（2）同理有

        令

        同理可求得平面PA1B1的一个法向量   ………………10分

        要使平面PAB⊥平面PA1B1，只需则

          ………………11分

        解得： …………12分

    21．（理）解：（1）由条件得

       

       （2）①设直线m ……5分

       

        ②不妨设M，N的坐标分别为

    …………………8分

    因直线m的斜率不为零，故

       （文）解：（1）设  …………2分

       

        故所求双曲线方程为：

       （2）设，

       

        由焦点半径，  ………………8分

       

    22．（1）证明：

        所以在[0，1]上为增函数，   ………………3分

       （2）解：由

       

       （3）解：由（1）与（2）得 …………9分

        设存在正整数k，使得对于任意的正整数n，都有成立，

           ………………10分

       

        ，   ………………11分

        当，   ………………12分

        当    ………………13分

        所在存在正整数

        都有成立.   ………………14分

     

     

     

     


    同步练习册答案