
 ,其中
,其中 分别为甲、乙摸到的球的编号。
分别为甲、乙摸到的球的编号。 (3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)
(3,1),(3,2),(3,3),(3,4),(4,1),(4,2),(4,3),(4,4)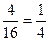 ………4分
………4分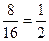 ………6分
………6分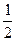 ,
,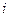 ”为事件
”为事件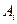 (
(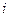 =2,3,4,5,6,7,8)………10分
=2,3,4,5,6,7,8)………10分

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
  | 200元 | 300元 | 400元 | 500元 |
| 老年 | 0.4 | 0.3 | 0.2 | 0.1 |
| 中年 | 0.3 | 0.4 | 0.2 | 0.1 |
| 青年 | 0.3 | 0.3 | 0.2 | 0.2 |
 ,求
,求 的分布列及数学期望。
的分布列及数学期望。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 环数 | 7 | 8 | 9 | 10 |
| 命中次数 | 2 | 7 | 8 | 3 |
 次、
次、 次,每个基本事件为(m,n).求“
次,每个基本事件为(m,n).求“ ”的概率.
”的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,求抽奖者获奖的概率;
,求抽奖者获奖的概率; 表示获奖的人数,求
表示获奖的人数,求 的分布列及
的分布列及 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
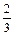 ,每次命中与否互相独立.
,每次命中与否互相独立.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com