
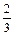 ,每次命中与否互相独立.
,每次命中与否互相独立. 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
 .,每次命中与否互相独立.
.,每次命中与否互相独立.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,其中
,其中 分别为甲、乙摸到的球的编号。
分别为甲、乙摸到的球的编号。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 动作 | K动作 | D动作 | ||
| 得分 | 100 | 80 | 40 | 10 |
| 概率 |  |  |  |  |
| 动作 | K动作 | D动作 | ||
| 得分 | 90 | 50 | 20 | 0 |
| 概率 |  |  |  |  |
 的分布列及数学期望
的分布列及数学期望
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
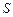 的正方形
的正方形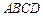 中有一个不规则的图形M,可按下面方法估计M的面积:在正方形
中有一个不规则的图形M,可按下面方法估计M的面积:在正方形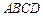 中随机投掷
中随机投掷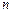 个点,若
个点,若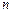 个点中有
个点中有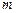 个点落入M中,则M的面积的估计值为
个点落入M中,则M的面积的估计值为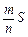 . 假设正方形
. 假设正方形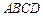 的边长为2,M的面积为1,并向正方形
的边长为2,M的面积为1,并向正方形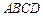 中随机投掷10 000个点,以
中随机投掷10 000个点,以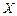 表示落入M中的点的数目.
表示落入M中的点的数目.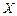 的均值
的均值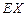 ;
; (Ⅱ)求用以上方法估计M的面积时,M的面积的估计值与实际值之差在区间
(Ⅱ)求用以上方法估计M的面积时,M的面积的估计值与实际值之差在区间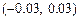 内的概率.
内的概率.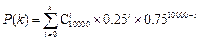
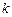 | 2424 | 2425 | 2574 | 2575 |
 | 0.0403 | 0.0423 | 0.9570 | 0.9590 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
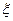 表示所选3人中女同学的人数.
表示所选3人中女同学的人数.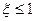 ,求共有不同选法的种数;
,求共有不同选法的种数; 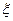 的分布列和数学期望;
的分布列和数学期望; 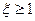 ”的概率.
”的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 个红球
个红球 和5个白球,一次摸奖从中摸两球,两个球颜色不同则为中奖。
和5个白球,一次摸奖从中摸两球,两个球颜色不同则为中奖。 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率 ;
; ,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率; ,当
,当 取多少时,
取多少时, 最大?
最大?查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.ab-a-b+1 | B.1-a-b | C.1-ab | D.1-2ab |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com