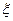练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    (本小题满分10分)
    某班从4名男同学和2名女同学中任选3人参加全校举行的“八荣八耻”教育演讲赛。如果设随机变量表示所选3人中女同学的人数.
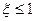    (1)若,求共有不同选法的种数;  
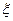    (2)求的分布列和数学期望； 
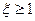    (3)求“”的概率.
    (1),所以共有不同选法的种数为16;                 …………2分
    (2)易知可能取的值为．
    所以，的分布列为

    		0
    		1
    		2
    P



     
    ………………………6分
    (3)的数学期望为：           ………………………8分
    (4)“所选3人中女同学人数”的概率为：          
     。                   ………………………10分
    略       
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：单选题

    如图所示，墙上挂有边长为a的正方形木板，它的四个角的空白部分都是以正方形的顶点为圆心，半径为的圆弧，某人向此板投镖，假设每次都能击中木板，且击中木板上每个点的可能性都一样，则它击中阴影部分的概率是                （   ）
    A．
    B．
    C．
    D．与a的值有关联

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）
    某设区举办2010年上海世博会知识宣传活动，进行现场抽奖，抽奖规则是：盒中装有10张大小相同的精美卡片，卡片上分别印有“世博会会徽”或“海宝”（世博会吉祥物）图案，参加者每次从盒中抽取卡片两张，若抽到两张都是“海宝”卡即可获奖。
    （I）活动开始后，一位参加者问：盒中有几张“海宝”卡？主持人笑说：我只知道若从盒总抽两张都不是“海宝”卡的概率是，求抽奖者获奖的概率；
    （Ⅱ）现有甲乙丙丁四人依次抽奖，抽后放回，另一个人再抽，用表示获奖的人数，求 的分布列及。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    (本小题满分12分)
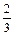    在一次抗洪抢险中，准备用射击的方法引爆从桥上游漂流而下的一巨大汽油罐.已知只有5发子弹备用，且首次命中只能使汽油流出，再次命中才能引爆成功，每次射击命中率都是，每次命中与否互相独立.
    (1) 求油罐被引爆的概率.
    (2) 如果引爆或子弹打光则停止射击，设射击次数为ξ，求ξ的分布列及ξ的数学期望。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分13分）
    甲乙两名射手互不影响地进行射击训练，根据以往的数据统计，他们设计成绩的分布列如下：
    射手甲
    		射手乙
    环数
    		8
    		9
    		10
    		环数
    		8
    		9
    		10
    概率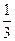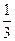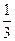



    		概率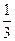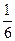



      （1）若甲射手共有5发子弹，一旦命中10环就停止射击，求他剩余3颗子弹的概率；
    （2）若甲乙两射手各射击两次，求四次射击中恰有三次命中10环的概率；
    （3）若两个射手各射击1次，记所得的环数之和为，求的分布列和期望。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题


    （理科做）
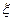    甲、乙两队进行一场排球比赛．根据以往经验，单局比赛甲队胜乙队的概率为0.6，本场比赛采用五局三胜制，即先胜三局的队获胜，比赛结束．设各局比赛相互间没有影响．令为本场比赛的局数．求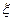的概率分布和数学期望．（精确到0.0001）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

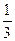    在某校运动会中，甲、乙、丙三支足球队进行单循环赛（即每两队比赛一场）共赛三场，每场比赛胜者得3分，负者得0分，没有平局。在每一场比赛中，甲胜乙的概率为，甲胜丙的概率为，乙胜丙的概率为；
    （Ⅰ）求甲队获第一名且丙队获第二名的概率；
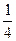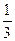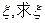    （Ⅱ）设在该次比赛中，甲队得分为的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    某人捡到不规则形状的五面体石块，他在每个面上用数字1～5进行了标记，投掷100次，记录下落在桌面上的数字，得到如下频数表：
    落在桌面的数字
    		1
    		2
    		3
    		4
    		5
    频数
    		32
    		18
    		15
    		13
    		22
    如果他再投掷一次，则落在桌面的数字不小于4的概率大约是
    A．0.22B．0.35 C．0.65D．0.78

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设随机变量X～B（n,p）,E(X)=12,D(X)=4,则n与p的值分别为 （     ）
    A．18，    B。12，   C，18，    D。12，

    查看答案和解析>>

    同步练习册答案