练习册

  • 练习册
  • 试题
    --5分又AB∩AV=A ∴AB⊥平面VAD----------6分 【查看更多】

     

    题目列表(包括答案和解析)

    设是两个不共线的非零向量.

    （1）若=，=，=，求证：A，B，D三点共线；

    （2）试求实数k的值，使向量和共线. (本小题满分13分)

    【解析】第一问利用=（）+（）+==得到共线问题。

    第二问，由向量和共线可知

    存在实数，使得=()

    =，结合平面向量基本定理得到参数的值。

    解：（1）∵=（）+（）+

    ==    ……………3分

    ∴      ……………5分

    又∵∴A，B，D三点共线   ……………7分

    （2）由向量和共线可知

    存在实数，使得=()   ……………9分

    ∴=   ……………10分

    又∵不共线

    ∴  ……………12分

    解得

     

    查看答案和解析>>

    设函数f(x)=x2+(lga+2)x+lgb，g(x)=2x+2，若f(－1)=0，且对一切实数x，不等式f(x)≥g(x)恒成立；

       （Ⅰ）（本问5分）求实数a、b的值；

       （Ⅱ）（本问7分）设F(x)=f(x)－g(x)，数列{an}满足关系an=F(n)，

             证明：

    查看答案和解析>>

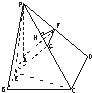    精英家教网如图，四棱锥P-ABCD的底面是矩形，PA⊥平面ABCD，E、F分别是AB、PD的中点，又二面角P-CD-B为45°．
    （1）求证：AF∥平面PEC；
    （2）求证：平面PEC⊥平面PCD；
    （3）设AD=2，CD=2
    		2
    ，求点A到平面PEC的距离．

    查看答案和解析>>

    如图，三棱锥A-BCD中，AB⊥平面BCD，BC=DC=1，∠BCD=90°，E，F分别是AC，AD上的动点，且EF∥平面BCD，二面角B-CD-A为60°．
    （1）求证：EF⊥平面ABC；k*s*5*u
    （2）若BE⊥AC，求直线BF与平面ACD所成角的余弦值．

    查看答案和解析>>

    给出下列命题：
    ①已知函数f(x)=(
    1
    2x-1
    )•x2-sinx+a(a为常数)    ，且f（loga1000）=3，则f（lglg2）=3；
    ②若函数f（x）=lg（x2+ax-a）的值域是R，则a∈（-4，0）；
    ③关于x的方程(
    1
    2
    )x=lga    有非负实数根，则实数a的取值范围是（1，10）；
    ④如图，三棱柱ABC-A1B1C1中，E、F分别是AB，AC的中点，平面EB1C1F将三棱柱分成几何体AEF-AB1C1和B1C1-EFCB两部分，其体积分别为V1，V2，则V1：V2=7：5．
    其中正确命题的序号是
    ①③④
    ①③④
    ．

    查看答案和解析>>


    同步练习册答案