
题目列表(包括答案和解析)
(本小题满分14分) 一圆形纸片的半径为10cm,圆心为O,
F为圆内一定点,OF=6cm,M为圆周上任意一点,把圆纸片折叠,
使M与F重合,然后抹平纸片,这样就得到一条折痕CD,设CD
与OM交于P点,如图
(1)求点P的轨迹方程;
(2)求证:直线CD为点P轨迹的切线.

(本小题满分14分)
一种计算装置,有一数据入口点A和一个运算出口点B ,按照某种运算程序:
①当从A口输入自然数1时,从B口得到 ,记为
,记为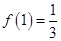 ;
;
②当从A口输入自然数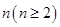 时,在B口得到的结果
时,在B口得到的结果 是前一个结果
是前一个结果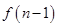 的
的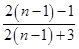 倍;
倍;
试问:当从A口分别输入自然数2 ,3 ,4 时,从B口分别得到什么数?试猜想 的关系式,并证明你的结论。
的关系式,并证明你的结论。
(本小题满分14分)
一种计算装置,有一数据入口点A和一个运算出口点B ,按照某种运算程序:
①当从A口输入自然数1时,从B口得到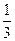 ,记为
,记为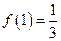 ;
;
② 当从A口输入自然数
当从A口输入自然数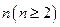 时,在B口得到的结果
时,在B口得到的结果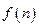 是前一个结果
是前一个结果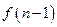 的
的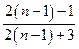 倍;
倍;
试问:当从A口分别输入自然数2 ,3 ,4 时,从B口分别得到什么数?试猜想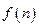 的关系式,并证明你的结论。
的关系式,并证明你的结论。
(本小题满分14分)一束光线从点![]() 出发,经直线
出发,经直线![]() 上一点
上一点![]() 反射后,恰好穿过点
反射后,恰好穿过点![]() .
.
(Ⅰ)求点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 的坐标;
的坐标;
(Ⅱ)求以![]() 、
、![]() 为焦点且过点
为焦点且过点![]() 的椭圆
的椭圆![]() 的方程;
的方程;
(Ⅲ)设直线![]() 与椭圆
与椭圆![]() 的两条准线分别交于
的两条准线分别交于![]() 、
、![]() 两点,点
两点,点![]() 为线段
为线段![]() 上的动点,求点
上的动点,求点![]() 到
到![]() 的距离与到椭圆
的距离与到椭圆![]() 右准线的距离之比的最小值,并求取得最小值时点
右准线的距离之比的最小值,并求取得最小值时点![]() 的坐标.
的坐标.
(本小题满分14分)
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
| 轿车A | 轿车B | 轿车C | |
| 舒适型 | 100 |
|
|
| 标准型 | 300 | 450 | 600 |
已知在该月生产的轿车中随机抽一辆,抽到舒适型轿车B的概率为0.075,按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1)求![]() 和
和![]() 的值;
的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com