（2012?丰台区一模）一质量M=0.8kg的小物块，用长l=0.8m的细绳悬挂在天花板上，处于静止状态．一质量m=0.2kg的粘性小球以速度v₀=10m/s水平射向物块，并与物块粘在一起，小球与物块相互作用时间极短可以忽略，不计空气阻力，重力加速度g取10m/s²．求：
（1）小球粘在物块上的瞬间，小球和物块共同速度的大小；
（2）小球和物块摆动过程中，细绳拉力的最大值；
（3）小球和物块摆动过程中所能达到的最大高度．

（2011?丰台区二模）如图所示，竖直平面内有四分之一圆弧轨道固定在水平桌面上，圆心为O点．一小滑块自圆弧轨道A处由静止开始自由滑下，在B点沿水平方向飞出，落到水平地面C点．已知小滑块的质量为m=1.0kg，C点与B点的水平距离为1.0m，B点高度为1.25m，圆弧轨道半径R=1.0m，取g=10m/s²．求小滑块：
（1）从B点飞出时的速度大小；
（2）在B点时对圆弧轨道的压力大小；
（3）沿圆弧轨道下滑过程中克服摩擦力所做的功．

（2009?丰台区一模）（1）在《验证机械能守恒定律》的实验中，已知重锤的质量为m，使用的交流电的频率为f．重锤从高处由静止开始下落，重锤上拖着的纸带通过打点计时器打出一系列的点，对纸带上的点进行测量并通过计算，就可以验证机械能守恒定律．
①如图1所示，选取纸带上打出的连续五个点A、B、C、D、E，测出A点距起始点O的距离为s₀，点A、C间的距离为s₁，点C、E间的距离为s₂，用以上给出的已知量写出C点速度的表达式为υ_c=，打点计时器在打O点到C点的这段时间内，重锤的重力势能的减少量为，动能的增加量为．
②某同学上交的实验报告显示，重锤增加的动能略大于重锤减小的重力势能，则出现这一问题的原因可能是．（填字母）
A．重锤的质量测量错误
B．该同学自编了实验数据
C．该同学实验操作时先释放纸带，后接通电源
D．重锤下落时受到的阻力过大

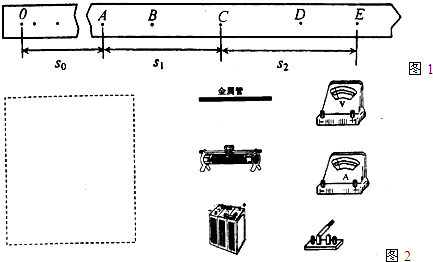
（2）有一根很细的均匀空心金属管，管长约50cm、电阻约为10Ω，现需测定它的内径d，但因其内径较小，无法用游标卡尺直接测量．已知这种金属的电阻率为ρ．实验室中可以提供下列器材：
A．厘米刻度尺；   B．毫米刻度尺；
C．螺旋测微器；   D．电流表（量程300mA，内阻约lΩ）；
E．电流表（量程3A，内阻约0．lΩ）”；   F．电压表（量程3V，内阻约6kΩ）；
G．滑动变阻器（最大阻值1kΩ，额定电流0.5A）；
H．滑动变阻器（最大阻值5Ω，额定电流2A）；
L．蓄电池（电动势6V，内阻0.05Ω）；J．开关一个及带夹子的导线若干．
请设计一个实验方案，要求实验误差小，便于调节．回答下列问题：
①实验中应测物理量的名称及符号是；
②应选用的实验器材有；（填字母）
③在图2所示的方框中画出实验电路图；
④按照你设计的电路图将图2中所示仪器连成实验电路；
⑤用测得的物理量和已知量写出计算金属管内径d的表达式为d=．

（2011?丰台区一模）1932年美国物理学家劳伦斯发明了回旋加速器，巧妙地利用带电粒子在磁场中的运动特点，解决了粒子的加速问题．现在回旋加速器被广泛应用于科学研究和医学设备中．

某型号的回旋加速器的工作原理如图甲所示，图为俯视图乙．回旋加速器的核心部分为D形盒，D形盒装在真空容器中，整个装置放在巨大的电磁铁两极之间的强大磁场中，磁场可以认为是匀强在场，且与D形盒盒面垂直．两盒间狭缝很小，带电粒子穿过的时间可以忽略不计．D形盒半径为R，磁场的磁感应强度为B．设质子从粒子源A处时入加速电场的初速度不计．质子质量为m、电荷量为+q．加速器接一定涉率高频交流电源，其电压为U．加速过程中不考虑相对论效应和重力作用．
（1）求质子第1次经过狭缝被加速后进入D形盒运动轨道的半径r₁；
（2）求质子从静止开始加速到出口处所需的时间t；
（3）如果使用这台回旋加速器加速α粒子，需要进行怎样的改动？请写出必要的分析及推理．

（2008?丰台区一模）如图所示，光滑的圆弧轨道AB、EF，半径AO、O′F均为R且水平．质量为m、长度也为R的小车静止在光滑水平面CD上，小车上表面与轨道AB、EF的末端B、E相切．一质量为m的物体（可视为质点）从轨道AB的A点由静止下滑，由末端B滑上小车，小车立即向右运动．当小车右端与壁DE刚接触时，物体m恰好滑动到小车右端且相对于小车静止，同时小车与壁DE相碰后立即停止运动但不粘连，物体继续运动滑上圆弧轨道EF，以后又滑下来冲上小车．求：

（1）水平面CD的长度和物体m滑上轨道EF的最高点相对于E点的高度h；
（2）当物体再从轨道EF滑下并滑上小车后，小车立即向左运动．如果小车与壁BC相碰后速度也立即变为零，最后物体m停在小车上的Q点，则Q点距小车右端多远？