
题目列表(包括答案和解析)
 A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线ρsin(θ+
A.(选修4-4坐标系与参数方程)已知点A是曲线ρ=2sinθ上任意一点,则点A到直线ρsin(θ+| π | 3 |
 A.(不等式选做题)若关于x的不等式|x+3|-|x+2|≥log2a有解,则实数a的取值范围是:
A.(不等式选做题)若关于x的不等式|x+3|-|x+2|≥log2a有解,则实数a的取值范围是:| PB |
| PA |
| 1 |
| 2 |
| PC |
| PD |
| 1 |
| 3 |
| BC |
| AD |
|
| 2 |
| cosθ-sinθ |
| 2 |
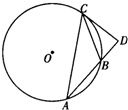 A.(不等式选做题)
A.(不等式选做题)| 3 |
| π |
| 3 |
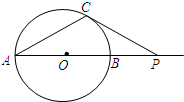 A.不等式
A.不等式| x-2 |
| x2+3x+2 |
| 3 |
|
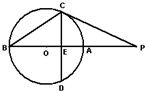 A.(不等式选做题)不等式|3x-6|-|x-4|>2x的解集为
A.(不等式选做题)不等式|3x-6|-|x-4|>2x的解集为| π |
| 4 |
| 2 |
一、选择题(本大题共10小题,每小题5分,共50分)
1―5 ABCDC 6―10 CDBAB
二、填空题(本大题共7小题,每小题4分,共28分)
11. 12.
12. 13.10 14.
13.10 14. 15.1 16.50 17.―1
15.1 16.50 17.―1
三、解答题(本大题共5小题,共72分。解答应写出文字说明、证明过程或演算过程)
18.(本小题满分14分)
解:(I) ………………3分
………………3分
 ………………5分
………………5分
 ………………8分
………………8分
(II)由(I)可得 …………14分
…………14分
19.(本小题满分14分)
解:(I)由 从而
从而

(II) ,
,
 ………………11分
………………11分
若 ………………14分
………………14分
20.(本小题满分14分)
解:(1)在D1B1上取点M,使D1M=1,
连接MB,MF。 ………………1分
∵D1F=1,D1M=1,
|