
题目列表(包括答案和解析)
(理)已知数列{an}的前n项和 ,且
,且 =1,
=1,
 .
.
(I)求数列{an}的通项公式;
(II)已知定理:“若函数f(x)在区间D上是凹函数,x>y(x,y∈D),且f’(x)存在,则有
< f’(x)”.若且函数y=xn+1 在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
在(0,+∞)上是凹函数,试判断bn与bn+1的大小;
(III)求证:≤bn<2.
 (文)如图,|AB|=2,O为AB中点,直线
(文)如图,|AB|=2,O为AB中点,直线 过B且垂直于AB,过A的动直线与
过B且垂直于AB,过A的动直线与 交于点C,点M在线段AC上,满足=.
交于点C,点M在线段AC上,满足=.
(I)求点M的轨迹方程;
(II)若过B点且斜率为- 的直线与轨迹M交于
点P,点Q(t,0)是x轴上任意一点,求当ΔBPQ为
锐角三角形时t的取值范围.
已知数列 是首项为
是首项为 的等比数列,且满足
的等比数列,且满足
 .
.
(1) 求常数 的值和数列
的值和数列 的通项公式;
的通项公式;
(2) 若抽去数列 中的第一项、第四项、第七项、……、第
中的第一项、第四项、第七项、……、第 项、……,余下的项按原来的顺序组成一个新的数列
项、……,余下的项按原来的顺序组成一个新的数列 ,试写出数列
,试写出数列 的通项公式;
的通项公式;
(3) 在(2)的条件下,设数列 的前
的前 项和为
项和为 .是否存在正整数
.是否存在正整数 ,使得
,使得 ?若存在,试求所有满足条件的正整数
?若存在,试求所有满足条件的正整数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【解析】第一问中解:由 得
得 ,,
,,
又因为存在常数p使得数列 为等比数列,
为等比数列,
则 即
即 ,所以p=1
,所以p=1
故数列 为首项是2,公比为2的等比数列,即
为首项是2,公比为2的等比数列,即 .
.
此时 也满足,则所求常数
也满足,则所求常数 的值为1且
的值为1且
第二问中,解:由等比数列的性质得:
(i)当 时,
时, ;
;
(ii) 当 时,
时, ,
,
所以
第三问假设存在正整数n满足条件,则 ,
,
则(i)当 时,
时,
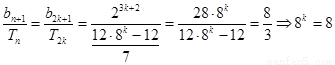
 ,
,
| n |
 |
| i=1 |
| n |
 |
| i=1 |
| n |
 |
| i=1 |
一、选择题(本大题共10小题,每小题5分,共50分)
1―5 ABCDC 6―10 CDBAB
二、填空题(本大题共7小题,每小题4分,共28分)
11. 12.
12. 13.10 14.
13.10 14. 15.1 16.50 17.―1
15.1 16.50 17.―1
三、解答题(本大题共5小题,共72分。解答应写出文字说明、证明过程或演算过程)
18.(本小题满分14分)
解:(I) ………………3分
………………3分
 ………………5分
………………5分
 ………………8分
………………8分
(II)由(I)可得 …………14分
…………14分
19.(本小题满分14分)
解:(I)由 从而
从而

(II) ,
,
 ………………11分
………………11分
若 ………………14分
………………14分
20.(本小题满分14分)
解:(1)在D1B1上取点M,使D1M=1,
连接MB,MF。 ………………1分
∵D1F=1,D1M=1,
|